Refine listing
Actions for selected content:
291 results in 46Bxx
ON VON NEUMANN–JORDAN CONSTANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 371-375
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
FLAT SETS, ℓp-GENERATING AND FIXING c0 IN THE NONSEPARABLE SETTING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 197-210
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
OPTIMAL LOWER BOUND ON THE SUPREMAL STRICT p-NEGATIVE TYPE OF A FINITE METRIC SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 19 August 2009, pp. 486-497
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
NONEXPANSIVE MAPPINGS ON THE UNIT SPHERES OF SOME BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 139-146
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
MEASURES OF NONCOMPACTNESS IN ULTRAPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 165-172
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
Dependence of the Weyl coefficient on singular interface conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 445-487
-
- Article
-
- You have access
- Export citation
Amenability of ultrapowers of Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 307-338
-
- Article
-
- You have access
- Export citation
A NEW CHARACTERIZATION OF REFLEXIVITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 443-444
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
VECTOR SUBSPACES OF THE SET OF NON-NORM-ATTAINING FUNCTIONALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 425-432
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
INEQUALITIES FOR SUPERADDITIVE FUNCTIONALS WITH APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 401-411
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
OPERATORS ON C0(L,X) WHOSE RANGE DOES NOT CONTAIN c0
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 515-520
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Extrapolation of the functional calculus of generalized Dirac operators and related embedding and Littlewood-Paley-type theorems. I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-326
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Linearization of certain uniform homeomorphisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-9
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Semicontinuous functions and convex sets in C(K) spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-121
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Connection Between Strong and Norming Markushevich Bases in Non-Separable Banach Spaces
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 321-328
- Print publication:
- December 2006
-
- Article
- Export citation
Smooth Partitions of Unity on Certain C(K) Spaces
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 131-138
- Print publication:
- December 2005
-
- Article
- Export citation
Some questions about rotundity and renormings in Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-140
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
A dual differentiation space without an equivalent locally uniformly rotund norm
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
The strong closure of Boolean algebras of projections in Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-370
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Operator-valued multiplier theorems characterizing Hilbert spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-184
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
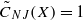 that is not isomorphic to any Hilbert space, where
that is not isomorphic to any Hilbert space, where 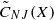 denotes the infimum of all von Neumann–Jordan constants for equivalent norms of
denotes the infimum of all von Neumann–Jordan constants for equivalent norms of 
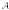 is Arens regular, and give some evidence that this is so if and only if
is Arens regular, and give some evidence that this is so if and only if  of non-norm-attaining functionals on
of non-norm-attaining functionals on 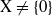 is a Banach space and (
is a Banach space and (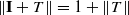 ; (b) if Γ is a nonempty set and
; (b) if Γ is a nonempty set and 