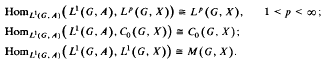Refine listing
Actions for selected content:
291 results in 46Bxx
Some trigonometric extremal problems and duality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-390
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Riesz sets and the Radon-Nikodym property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-308
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
A locally uniformly convex renorming for certain ℒ(K)
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-8
- Print publication:
- June 1990
-
- Article
- Export citation
Some examples concerning normal and uniform normal structure in Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-234
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
Linear operators in l2 with a universality property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-222
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
On the geometry of spheres in normed linear spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 101-112
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Generic well-posedness of optimization problems in topological spaces
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 301-324
- Print publication:
- December 1989
-
- Article
- Export citation
Normal Structure for Banach Spaces with Schauder Decomposition
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-351
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
A Dual characterization of Banach Spaces With the Convex Point-of-Continuity Property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 274-280
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
The two-ball property: transitivity and examples
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-197
- Print publication:
- December 1988
-
- Article
- Export citation
Monotonic norms in ordered Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-219
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
On the length of faithful nuclear representations of finite rank operators
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 1 / June 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 126-143
- Print publication:
- June 1988
-
- Article
- Export citation
Internal characterization of fragmentable spaces
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 243-257
- Print publication:
- December 1987
-
- Article
- Export citation
Radon-Nikodým compact spaces and fragmentability
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-281
- Print publication:
- December 1987
-
- Article
- Export citation
Inscribed centers, reflexivity, and some applications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-324
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Completeness of normed linear spaces admitting centers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 360-366
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Borel selectors for upper semi-continuous multi-valued functions
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 324-337
- Print publication:
- December 1985
-
- Article
- Export citation
Multipliers of Banach valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-62
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Measures coniques sur un espace de Banach ou son dual
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Rotundity redux
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-151
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
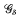 -subset of
-subset of 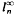 are proved.
are proved.