Refine listing
Actions for selected content:
291 results in 46Bxx
Three space property for σ-fragmentability
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-118
- Print publication:
- June 1998
-
- Article
- Export citation
Generic continuity of minimal set-valued mappings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-262
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
HB-subspaces and Godun sets of subspaces in Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-132
- Print publication:
- June 1997
-
- Article
- Export citation
Almost Fréchet differentiability of finitely many Lipschitz functions
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 393-412
- Print publication:
- December 1996
-
- Article
- Export citation
On C2-smooth norms on c0
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 362-370
- Print publication:
- December 1996
-
- Article
- Export citation
Isometries of Hilbert space valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 150-161
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
σ-fragmentability and analyticity
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-181
- Print publication:
- June 1996
-
- Article
- Export citation
The uniform Kadec-Klee property for the Lorentz spaces Lw,1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-17
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
On the uniform Kadec-Klee property with respect to convergence in measure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-352
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Baire trees, bad norms and the Namioka property
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-42
- Print publication:
- June 1995
-
- Article
- Export citation
Lp-Lq estimates off the line of duality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 154-166
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
On uniformly Gâteaux differentiable norms in C(K)
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-238
- Print publication:
- December 1994
-
- Article
- Export citation
Random Banach spaces: The limitations of the method
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-250
- Print publication:
- December 1994
-
- Article
- Export citation
Borel and analytic sets in Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-140
- Print publication:
- June 1994
-
- Article
- Export citation
The weak drop property on closed convex sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-130
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Smooth bump functions and geomentry of Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-321
- Print publication:
- December 1993
-
- Article
- Export citation
Rosenthal sets and the Radon-Nikodym property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-220
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Biduals of weighted banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 70-79
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
σ-fragmentable Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-188
- Print publication:
- June 1992
-
- Article
- Export citation
Mosco convergence and weak topologies for convex sets and functions
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-104
- Print publication:
- June 1991
-
- Article
- Export citation
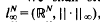 , or equivalently, -typical
, or equivalently, -typical 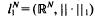 , where the meaning of what is typical and what is not is defined in terms of the Haar measure
, where the meaning of what is typical and what is not is defined in terms of the Haar measure 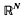 .
.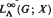 is separable then
is separable then 
 is any family of subsets of
is any family of subsets of 