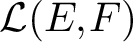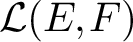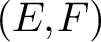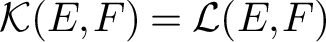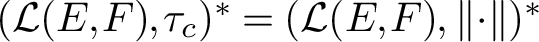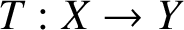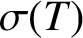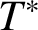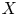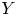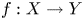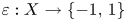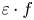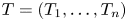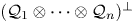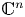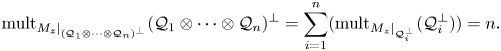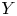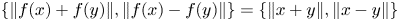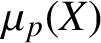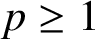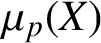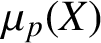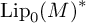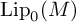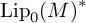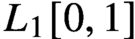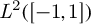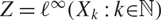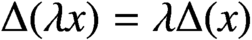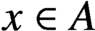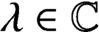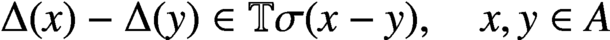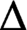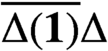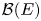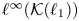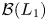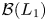Refine listing
Actions for selected content:
292 results in 46Bxx
APPROXIMATELY MULTIPLICATIVE DECOMPOSITIONS OF NUCLEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 314-322
- Print publication:
- April 2022
-
- Article
- Export citation
ON THE EXISTENCE OF NON-NORM-ATTAINING OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 July 2021, pp. 1023-1035
- Print publication:
- May 2023
-
- Article
- Export citation
EQUIVALENCE OF SEMI-NORMS RELATED TO SUPER WEAKLY COMPACT OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 506-518
- Print publication:
- December 2021
-
- Article
- Export citation
RETRACTED – The wigner property for CL-spaces and finite-dimensional polyhedral banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 717-733
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
The wigner property for CL-spaces and finite-dimensional polyhedral Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 183-199
-
- Article
- Export citation
REVISITING THE RECTANGULAR CONSTANT IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 124-133
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
NORMAL FUNCTIONALS ON LIPSCHITZ SPACES ARE WEAK* CONTINUOUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2093-2102
- Print publication:
- November 2022
-
- Article
- Export citation
SUBPROJECTIVITY OF PROJECTIVE TENSOR PRODUCTS OF BANACH SPACES OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 31 March 2021, pp. 292-305
-
- Article
- Export citation
CARLESON INTERPOLATING SEQUENCES FOR BANACH SPACES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1915-1945
- Print publication:
- November 2022
-
- Article
- Export citation
A ξ-weak Grothendieck compactness principle
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 10 March 2021, pp. 231-246
- Print publication:
- January 2022
-
- Article
- Export citation
Uniformly factoring weakly compact operators and parametrised dualisation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 March 2021, e22
-
- Article
-
- You have access
- Open access
- Export citation
THE METRIC PROJECTIONS ONTO CLOSED CONVEX CONES IN A HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 1617-1650
- Print publication:
- September 2022
-
- Article
- Export citation
The factorisation property of l∞(Xk)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 10 December 2020, pp. 421-448
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
A SPHERICAL VERSION OF THE KOWALSKI–SŁODKOWSKI THEOREM AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 386-411
-
- Article
- Export citation
A short proof that ℬ(L1) is not amenable
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 1758-1767
- Print publication:
- December 2021
-
- Article
- Export citation
ON THE COMPLEXITY OF CLASSIFYING LEBESGUE SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1254-1288
- Print publication:
- September 2020
-
- Article
- Export citation
On the von Neumann algebras associated to Yang–Baxter operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 1331-1354
- Print publication:
- August 2021
-
- Article
- Export citation
ON THE STABILITY OF THE DIFFERENTIAL PROCESS GENERATED BY COMPLEX INTERPOLATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 303-334
- Print publication:
- January 2022
-
- Article
- Export citation
On decay rates of the solutions of parabolic Cauchy problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 1021-1039
- Print publication:
- June 2021
-
- Article
- Export citation