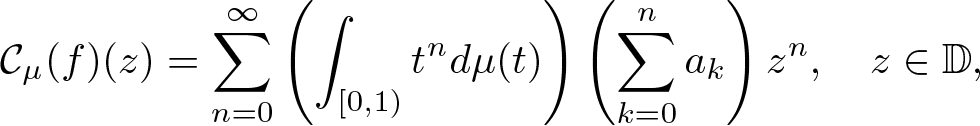Refine listing
Actions for selected content:
96 results in 30Hxx
Note on real and imaginary parts of harmonic quasiregular mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 25 September 2025, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuity and realization of multiplicative maps between RKHS and their cyclicity preserving properties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-14
-
- Article
- Export citation
A Cesàro-like operator from a class of analytic function spaces to analytic Besov spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1210-1222
- Print publication:
- December 2025
-
- Article
- Export citation
A note on composition operators on the disc and bidisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1163-1176
- Print publication:
- December 2025
-
- Article
- Export citation
FINITE LINEAR COMBINATIONS OF MONOMIAL TOEPLITZ PRODUCTS ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 39-60
- Print publication:
- August 2025
-
- Article
- Export citation
Isometric dilation and Sarason’s commutant lifting theorem in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1-33
-
- Article
- Export citation
Cyclicity of the shift operator through Bezout identities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 January 2025, pp. 684-708
- Print publication:
- September 2025
-
- Article
- Export citation
Elliptic hyperlogarithms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-36
-
- Article
-
- You have access
- HTML
- Export citation
New aspects of Bargmann transform using Touchard polynomials and hypergeometric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-46
-
- Article
- Export citation
Nearly invariant Brangesian subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 318-337
- Print publication:
- March 2025
-
- Article
- Export citation
Complex linear differential equations with solutions in weighted Dirichlet spaces and derivative Hardy spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 653-666
- Print publication:
- September 2025
-
- Article
- Export citation
Hilbert matrix operator acting between conformally invariant spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 550-567
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert type operators acting from the Bloch space into Bergman spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 205-225
-
- Article
- Export citation
Cesàro-type operators on Bergman–Morrey spaces and Dirichlet–Morrey spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 268-299
-
- Article
- Export citation
A note on the space of all Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 November 2024, pp. 1123-1140
- Print publication:
- December 2024
-
- Article
- Export citation
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 927-935
- Print publication:
- December 2024
-
- Article
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 749-777
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1546-1569
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1093-1134
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASS OF SYMBOLS THAT INDUCE BOUNDED COMPOSITION OPERATORS FOR DIRICHLET-TYPE SPACES ON THE DISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 March 2024, pp. 140-145
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation