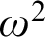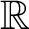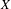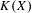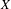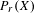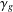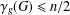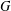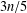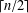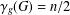Refine listing
Actions for selected content:
90 results in 91Axx
SHORTENING CLOPEN GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1541-1554
- Print publication:
- December 2021
-
- Article
- Export citation
Comparing the best-reply strategy and mean-field games: The stationary case
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 79-110
-
- Article
- Export citation
DOING WITHOUT ACTION TYPES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 380-410
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maker–Breaker percolation games I: crossing grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 200-227
-
- Article
-
- You have access
- Open access
- Export citation
Continuous-domain assignment flows
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 01 September 2020, pp. 570-597
-
- Article
- Export citation
GAME MODEL FOR ONLINE AND OFFLINE RETAILERS UNDER BUY-ONLINE AND PICK-UP-IN-STORE MODE WITH DELIVERY COST AND RANDOM DEMAND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 03 July 2020, pp. 62-88
-
- Article
-
- You have access
- Export citation
GAMES AND HEREDITARY BAIRENESS IN HYPERSPACES AND SPACES OF PROBABILITY MEASURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 June 2020, pp. 851-868
- Print publication:
- May 2022
-
- Article
- Export citation
THE VALUE OF COMMUNICATION AND COOPERATION WHEN SERVERS ARE STRATEGIC
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 06 April 2020, pp. 349-367
-
- Article
-
- You have access
- Export citation
Minimax functions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 06 December 2019, pp. 455-484
-
- Article
- Export citation
Two-player zero-sum stochastic differential games with random horizon
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1209-1235
- Print publication:
- December 2019
-
- Article
- Export citation
Persistence probability of a random polynomial arising from evolutionary game theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 870-890
- Print publication:
- September 2019
-
- Article
- Export citation
On the equivalence of mixed and behavior strategies in finitely additive decision problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 810-829
- Print publication:
- September 2019
-
- Article
- Export citation
A probabilistic verification theorem for the finite horizon two-player zero-sum optimal switching game in continuous time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 425-442
- Print publication:
- June 2019
-
- Article
- Export citation
THE DOMINATION GAME ON SPLIT GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 327-337
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Characterization and simplification of optimal strategies in positive stochastic games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 728-741
- Print publication:
- September 2018
-
- Article
- Export citation
A SIMULATION STUDY OF TEXAS HOLD ’EM POKER: WHAT TAYLOR SWIFT UNDERSTANDS AND JAMES BOND DOESN’T
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 08 August 2018, pp. 55-64
-
- Article
-
- You have access
- Export citation
Stochastic nonzero-sum games: a new connection between singular control and optimal stopping
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 347-372
- Print publication:
- June 2018
-
- Article
- Export citation
Nash equilibria for nonzero-sum ergodic stochastic differential games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 977-994
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
On zero-sum two-person undiscounted semi-Markov games with a multichain structure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 826-849
- Print publication:
- September 2017
-
- Article
- Export citation
Nash equilibrium in nonzero-sum games of optimal stopping for Brownian motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 430-445
- Print publication:
- June 2017
-
- Article
- Export citation