Refine listing
Actions for selected content:
221 results in 91Bxx
Monotone utility convergence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 622-633
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Large deviations for risk processes with reinsurance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-728
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Applications of factorization embeddings for Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 768-791
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
An optimal sequential procedure for a buying-selling problem with independent observations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 454-462
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
On extreme ruinous behaviour of Lévy insurance risk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 594-598
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Range of Asymptotic Behaviour of the Optimality Probability of the Expert and Majority Rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 16-31
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
On the expected time to ruin and the expected dividends when dividends are paid while the surplus is above a constant barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 595-607
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Conditional tail expectations for multivariate phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 810-825
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
The finite-time ruin probability of the compound Poisson model with constant interest force
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 608-619
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
What is the time value of a stream of investments?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 861-866
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Ruin in the perturbed compound Poisson risk process under interest force
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 819-835
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Differentiation of some functionals of risk processes, and optimal reserve allocation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 379-392
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Multiperiod conditional distribution functions for conditionally normal GARCH(1, 1) models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-445
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Explicit Bounds for Approximation Rates of Boundary Crossing Probabilities for the Wiener Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 82-92
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Kalman-Bucy Filtering for Linear Systems Driven by the Cox Process with Shot Noise Intensity and Its Application to the Pricing of Reinsurance Contracts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 93-107
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Electronic Foreign-Exchange Markets and Passage Events of Independent Subordinators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 138-152
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Finite- and infinite-time ruin probabilities in the presence of stochastic returns on investments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1278-1299
- Print publication:
- December 2004
-
- Article
- Export citation
A continuous-time GARCH process driven by a Lévy process: stationarity and second-order behaviour
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-622
- Print publication:
- September 2004
-
- Article
- Export citation
Ruin probabilities for competing claim processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 679-690
- Print publication:
- September 2004
-
- Article
- Export citation
On the subexponential properties in stationary single-server queues: a Palm-martingale approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 872-892
- Print publication:
- September 2004
-
- Article
- Export citation
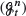 be a sequence of increasing filtrations converging to
be a sequence of increasing filtrations converging to 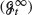 , and let
, and let 