We prove that if a space $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}X$ with a rank 2-diagonal either has the countable chain condition or is star countable then the cardinality of $X$ is at most $\mathfrak{c}$.

We mainly prove that, assuming $\mathfrak{b}= \mathfrak{c}$, every regular star-compact space with a strong rank 1-diagonal is metrisable.

It is proved that every remainder of a nonlocally compact semitopological group $G$ is a Baire space if and only if $G$ is not Čech-complete, which improves a dichotomy theorem of topological groups by Arhangel’skiǐ [‘The Baire property in remainders of topological groups and other results’, Comment. Math. Univ. Carolin. 50(2) (2009), 273–279], and also gives a positive answer to a question of Lin and Lin [‘About remainders in compactifications of paratopological groups’, ArXiv: 1106.3836v1 [Math. GN] 20 June 2011]. We also show that for a nonlocally compact rectifiable space $G$ every remainder of $G$ is either Baire, or meagre and Lindelöf.

Let $G$ be a locally compact group. In this paper, we show that if $G$ is a nondiscrete locally compact group, $p\in (0, 1)$ and $q\in (0, + \infty ] $, then $\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\text{ is finite } \lambda \text{-a.e.} \} $ is a set of first category in ${L}^{p} (G)\times {L}^{q} (G)$. We also show that if $G$ is a nondiscrete locally compact group and $p, q, r\in [1, + \infty ] $ such that $1/ p+ 1/ q\gt 1+ 1/ r$, then $\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\in {L}^{r} (G)\} $, is a set of first category in ${L}^{p} (G)\times {L}^{q} (G)$. Consequently, for $p, q\in [1+ \infty )$ and $r\in [1, + \infty ] $ with $1/ p+ 1/ q\gt 1+ 1/ r$, $G$ is discrete if and only if ${L}^{p} (G)\ast {L}^{q} (G)\subseteq {L}^{r} (G)$; this answers a question raised by Saeki [‘The ${L}^{p} $-conjecture and Young’s inequality’, Illinois J. Math. 34 (1990), 615–627].

We study the relationship between generalisations of P-spaces and Volterra (weakly Volterra) spaces, that is, spaces where every two dense Gδ have dense (nonempty) intersection. In particular, we prove that every dense and every open, but not every closed subspace of an almost P-space is Volterra and that there are Tychonoff nonweakly Volterra weak P-spaces. These results should be compared with the fact that every P-space is hereditarily Volterra. As a byproduct we obtain an example of a hereditarily Volterra space and a hereditarily Baire space whose product is not weakly Volterra. We also show an example of a Hausdorff space which contains a nonweakly Volterra subspace and is both a weak P-space and an almost P-space.

In this paper we give a lower bound on the waist of the unit sphere of a uniformly convex normed space by using the localization technique in codimension greater than one and a strong version of the Borsuk–Ulam theorem. The tools used in this paper follow ideas of Gromov in [Isoperimetry of waists and concentration of maps, Geom. Funct. Anal. 13 (2003), 178–215] and we also include an independent proof of our main theorem which does not rely on Gromov’s waist of the sphere. Our waist inequality in codimension one recovers a version of the Gromov–Milman inequality in [Generalisation of the spherical isoperimetric inequality to uniformly convex Banach spaces, Compositio Math. 62 (1987), 263–282].

We demonstrate a construction that will densely embed a Moore space into a Moore space with the Baire property when this is possible. We also show how this technique generates a new ‘if and only if’ condition for determining when Moore spaces can be densely embedded in Moore spaces with the Baire property, and briefly discuss how this condition can can be used to generate new proofs that certain Moore spaces cannot be densely embedded in Moore spaces with the Baire property.

van Mill et al. posed in ‘Classes defined by stars and neighborhood assignments’, Topology Appl.154 (2007), 2127–2134 the following question: Is a star-compact space metrizable if it has a Gδ-diagonal? In this paper, we give a negative answer to this question.

To each filter ℱ on ω, a certain linear subalgebra A(ℱ) of Rω, the countable product of lines, is assigned. This algebra is shown to have many interesting topological properties, depending on the properties of the filter ℱ. For example, if ℱ is a free ultrafilter, then A(ℱ) is a Baire subalgebra of ℱω for which the game OF introduced by Tkachenko is undetermined (this resolves a problem of Hernández, Robbie and Tkachenko); and if ℱ1 and ℱ2 are two free filters on ω that are not near coherent (such filters exist under Martin's Axiom), then A (ℱ1) and A(ℱ2) are two o-bounded and OF-undetermined subalgebras of ℱω whose product A(ℱ1) × A(ℱ2) is OF-determined and not o-bounded (this resolves a problem of Tkachenko). It is also shown that the statement that the product of two o-bounded subrings of ℱω is o-bounded is equivalent to the set-theoretic principle NCF (Near Coherence of Filters); this suggests that Tkachenko's question on the productivity of the class of o-bounded topological groups may be undecidable in ZFC.

In this work we study the structure of approximate solutions of variational problems with continuous integrands f: [0, ∞) × Rn × Rn → R1 which belong to a complete metric space of functions. The main result in this paper deals with the turnpike property of variational problems. To have this property means that the approximate solutions of the problems are determined mainly by the integrand, and are essentially independent of the choice of interval and endpoint conditions, except in regions close to the endpoints.

The following conjecture generalizing the Contraction Mapping Theorem was made by Stein.

Let (X, ρ) be a complete metric space and let ℱ = {T1,…, Tn} be a finite family of self-maps of X. Suppose that there is a constant γ ∈ (0, 1) such that, for any x, y ∈ X, there exists T ∈ ℱ with ρ(T(x), T(y)) ≤ γρ(x, y). Then some composition of members of ℱ has a fixed point.

In this paper this conjecture is disproved, We also show that it does hold for a (continuous) commuting ℱ in the case n = 2. It is conjectured that it holds for commuting ℱ for any n.

In this paper, we investigate Volterra spaces and relevant topological properties. New characterizations of weakly Volterra spaces are provided. An analogy of the Banach category theorem in terms of Volterra properties is obtained. It is shown that every weakly Volterra homogeneous space is Volterra, and there are metrizable Baire spaces whose hyperspaces of nonempty compact subsets endowed with the Vietoris topology are not weakly Volterra.

In this paper, we present some new metrization theorems in terms of Heath g–functions.

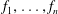
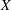
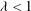
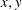
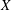
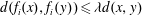
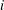
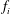
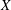
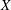
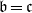
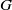
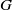
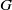
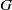
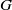
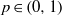
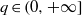
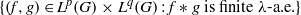
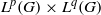
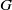
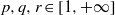
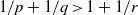
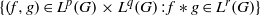
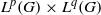
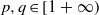
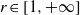
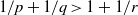
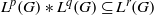
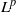
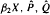In this paper we study the Stone-Čech bicompactification () of the bispace (X, P, Q). We show that the ring of all continuous real-valued functions on (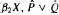) may be identified with the uniform closure of a suitable subring of 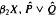C(). Using this result, we give a characterization of the Wallman-Sanin compactifications of the pairwise Tychonoff bitopological spaces.

A probabilistic convergence structure assigns a probability that a given filter converges to a given element of the space. The role of the t-norm (triangle norm) in the study of regularity of probabilistic convergence spaces is investigated. Given a probabilistic convergence space, there exists a finest T-regular space which is coarser than the given space, and is referred to as the ‘T-regular modification’. Moreover, for each probabilistic convergence space, there is a sequence of spaces, indexed by nonnegative ordinals, whose first term is the given space and whose last term is its T-regular modification. The T-regular modification is illustrated in the example involving ‘convergence with probability λ’ for several t-norms. Suitable function space structures in terms of a given t-norm are also considered.

The aim of this paper is to explore some properties of quasiuniform multifunction spaces. Various kinds of completeness of the quasiuniform multifunction space (YmX, UmX) are characterized in terms of suitable properties of the range space (Y, U). We also discuss the local compactness of quasiuniform multifunction spaces. By using the notion of small-set symmetry, the classic result of Hunsaker and Naimpally is extended to the quasiuniform setting.

A basic theory for probabilistic convergence spaces based on filter convergence is introduced. As in Florescu's previous theory of probabilistic convergence structures based on nets, one is able to assign a probability that a given filter converges to a given point. Various concepts and theorems pertaining to convergence spaces are extended to the realm of probabilistic convergence spaces, and illustrated by means of examples based on convergence in probability and convergence almost everywhere. Diagonal axioms due to Kowalsky and Fischer are also studied, first for convergence spaces and then in the setting of probabilistic convergence spaces.

It is known that every frame is isomorphic to the generalized Gleason algebra of an essentially unique bi-Stonian space (X, σ, τ) in which σ is T0. Let (X, σ, τ) be as above. The specialization order ≤σ, of (X, σ) is τ × τ-closed. By Nachbin's Theorem there is exactly one quasi-uniformity U on X such that ∩U = ≤σ and J(U*) = τ. This quasi-uniformity is compatible with σ and is coarser than the Pervin quasi-uniformity U of (X, σ). Consequently, τ is coarser than the Skula topology of σ and coincides with the Skula topology if and only if U = P.

In this paper, the concept of essential equilibria for production economies is first given. We then prove that in ‘most’ production economies (in the sense of Baire category) all equilibria are essential.

In this paper we show that the Lorentz space Lw, 1(0, ∞) has the weak-star uniform Kadec-Klee property if and only if inft>0 (w(αt)/w(t)) > 1 and supt>0(φ(αt) / φ(t))< 1 for all α ∈ (0, 1), where φ(t) = ∫t0 w(s) ds.