Refine listing
Actions for selected content:
82 results in 54Exx
The uniform Kadec-Klee property for the Lorentz spaces Lw,1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-17
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
On different types of cleavability of topological spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-199
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Strongly zero-dimensional bispaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-337
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Some fixed point theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 304-312
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
On pairwise paracompactness
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-285
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Quasi θ-spaces and pairwise θ-perfect irreducible mappings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-333
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
On countably compact quasi-pseudometrizable spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-240
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Pairwise complete regularity as a separation axiom
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-245
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
Joins of topologies homeomorphic to the rationals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 256-262
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Characterizations of Quasi-Metrizable Bitopological Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 271-274
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
On the Bitopological Extension of the Bing Metrization Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-241
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
A new bitopological paracompactness
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 268-274
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A generalization of Tong's theorem and properties of pairwise perfectly normal spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-359
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
On bitopological quasi-pseudometrization
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 126-129
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
Two characterizations of quasi-pseudometrizable bitopological spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 3 / December 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-333
- Print publication:
- December 1983
-
- Article
-
- You have access
- Export citation
Nonexistence of universal paracompact M-spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-286
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation
A note on a paper by S. Lal
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-199
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation
On the order scale of a uniform space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 248-257
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
Topological properties of the scale of a uniform space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 1 / August 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 54-61
- Print publication:
- August 1982
-
- Article
-
- You have access
- Export citation
Uniform spaces, spanier quasitopologies, and a duality for locally convex algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 99-128
- Print publication:
- February 1980
-
- Article
-
- You have access
- Export citation
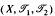 is quasi-metrizable if and only if for each point
is quasi-metrizable if and only if for each point  nbd bases {
nbd bases { 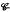 binary relations.
binary relations.