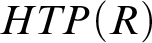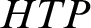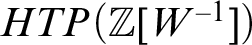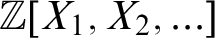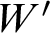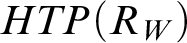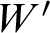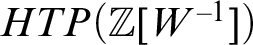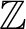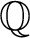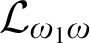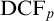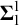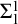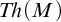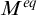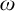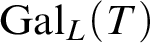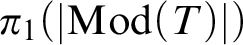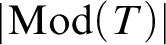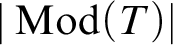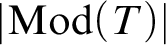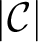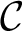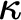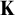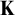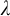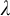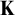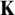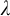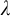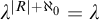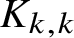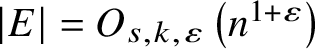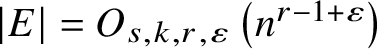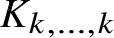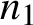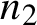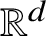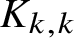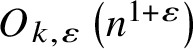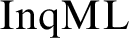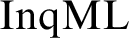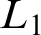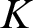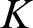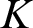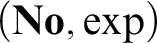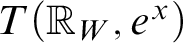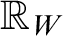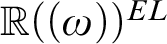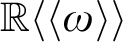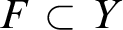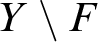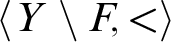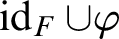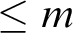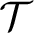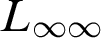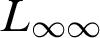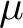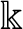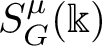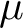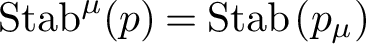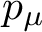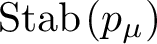Refine listing
Actions for selected content:
327 results in 03CXX
ON NON-COMPACT p-ADIC DEFINABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 November 2021, pp. 188-213
- Print publication:
- March 2022
-
- Article
- Export citation
HTP-COMPLETE RINGS OF RATIONAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 November 2021, pp. 252-272
- Print publication:
- March 2022
-
- Article
- Export citation
AN INTRODUCTION TO THE SCOTT COMPLEXITY OF COUNTABLE STRUCTURES AND A SURVEY OF RECENT RESULTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 November 2021, pp. 71-103
- Print publication:
- March 2022
-
- Article
- Export citation
MODEL THEORY OF DERIVATIONS OF THE FROBENIUS MAP REVISITED
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1213-1229
- Print publication:
- September 2023
-
- Article
- Export citation
FINITE RELATION ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 October 2021, pp. 874-888
- Print publication:
- June 2023
-
- Article
- Export citation
LOCALLY O-MINIMAL STRUCTURES WITH TAME TOPOLOGICAL PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 219-241
- Print publication:
- March 2023
-
- Article
- Export citation
DEGREE SPECTRA OF ANALYTIC COMPLETE EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1663-1676
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms yield upper bounds in differential algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 29-51
- Print publication:
- February 2023
-
- Article
- Export citation
MOST(?) THEORIES HAVE BOREL COMPLETE REDUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 September 2021, pp. 418-426
- Print publication:
- March 2023
-
- Article
- Export citation
CLASSIFYING SPACES AND THE LASCAR GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1396-1431
- Print publication:
- December 2021
-
- Article
- Export citation
RECONSTRUCTION OF NON-
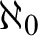 $\aleph _0$-CATEGORICAL THEORIES
$\aleph _0$-CATEGORICAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 159-187
- Print publication:
- March 2022
-
- Article
- Export citation
SOME STABLE NON-ELEMENTARY CLASSES OF MODULES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 93-117
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zarankiewicz’s problem for semilinear hypergraphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 31 August 2021, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FIRST-ORDER FRAMEWORK FOR INQUISITIVE MODAL LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 311-333
- Print publication:
- June 2022
-
- Article
- Export citation
FRAÏSSÉ LIMITS FOR RELATIONAL METRIC STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 August 2021, pp. 913-934
- Print publication:
- September 2021
-
- Article
- Export citation
SURREAL ORDERED EXPONENTIAL FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1066-1115
- Print publication:
- September 2021
-
- Article
- Export citation
VAUGHT’S CONJECTURE FOR ALMOST CHAINABLE THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 991-1005
- Print publication:
- September 2021
-
- Article
- Export citation
ASSOCIATIVITY OF THE MORLEY PRODUCT OF INVARIANT MEASURES IN NIP THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 12 August 2021, pp. 1293-1300
- Print publication:
- September 2021
-
- Article
- Export citation
LOGICALITY AND MODEL CLASSES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 385-414
- Print publication:
- December 2021
-
- Article
- Export citation
PETERZIL–STEINHORN SUBGROUPS AND
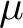 $\mu $-STABILIZERS IN ACF
$\mu $-STABILIZERS IN ACF
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 21 July 2021, pp. 1003-1022
- Print publication:
- May 2023
-
- Article
- Export citation