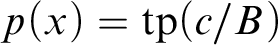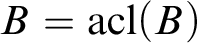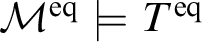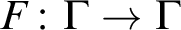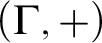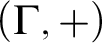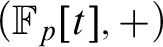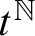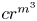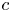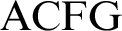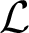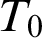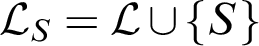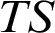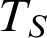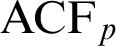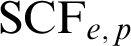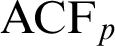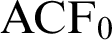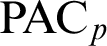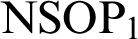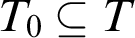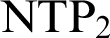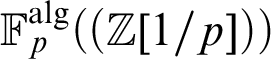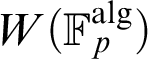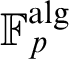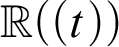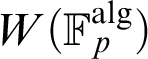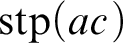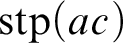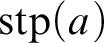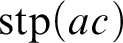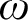Refine listing
Actions for selected content:
345 results in 03CXX
WEAK CANONICAL BASES IN NSOP
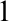 $_1$ THEORIES
$_1$ THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 June 2021, pp. 1259-1281
- Print publication:
- September 2021
-
- Article
- Export citation
THE POSET OF ALL LOGICS II: LEIBNIZ CLASSES AND HIERARCHY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 June 2021, pp. 324-362
- Print publication:
- March 2023
-
- Article
- Export citation
THE POSET OF ALL LOGICS I: INTERPRETATIONS AND LATTICE STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 935-964
- Print publication:
- September 2021
-
- Article
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
- Print publication:
- September 2021
-
- Article
- Export citation
CONTRIBUTIONS TO THE THEORY OF F-AUTOMATIC SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 127-158
- Print publication:
- March 2022
-
- Article
- Export citation
Smooth parameterizations of power-subanalytic sets and compositions of Gevrey functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 532-554
-
- Article
- Export citation
FORKING, IMAGINARIES, AND OTHER FEATURES OF
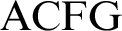 $\text {ACFG}$
$\text {ACFG}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 669-700
- Print publication:
- June 2021
-
- Article
- Export citation
Expansions and Neostability in Model Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 216-217
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Pseudofinite Structures and Counting Dimensions
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, p. 223
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Transfer Principles in Henselian Valued Fields
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 222-223
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Model Theory in a Paraconsistent Environment
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, p. 216
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
THE RELATIVIZED LASCAR GROUPS, TYPE-AMALGAMATION, AND ALGEBRAICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 531-557
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LATTICE OF SUPER-BELNAP LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 21 April 2021, pp. 114-163
- Print publication:
- March 2023
-
- Article
- Export citation
A CLASS OF FIELDS WITH A RESTRICTED MODEL COMPLETENESS PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 701-708
- Print publication:
- June 2021
-
- Article
- Export citation
RAMSEY’S COHEIRS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 377-391
- Print publication:
- March 2022
-
- Article
- Export citation
THICKET DENSITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 110-127
- Print publication:
- March 2021
-
- Article
- Export citation
ONE DIMENSIONAL GROUPS DEFINABLE IN THE p-ADIC NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 801-816
- Print publication:
- June 2021
-
- Article
- Export citation
RECURSIVE AXIOMATISATIONS FROM SEPARATION PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 03 February 2021, pp. 1228-1258
- Print publication:
- September 2021
-
- Article
- Export citation
TWO-VARIABLE LOGIC HAS WEAK, BUT NOT STRONG, BETH DEFINABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 785-800
- Print publication:
- June 2021
-
- Article
- Export citation
 $[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
$[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1632-1656
- Print publication:
- December 2021
-
- Article
- Export citation