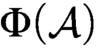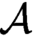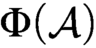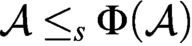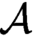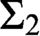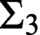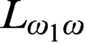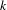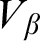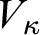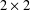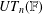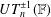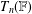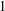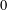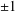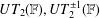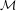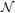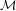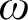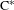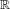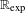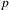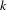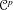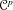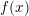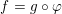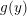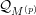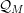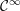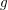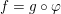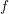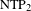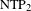Refine listing
Actions for selected content:
331 results in 03CXX
CODING IN GRAPHS AND LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 673-690
- Print publication:
- June 2020
-
- Article
- Export citation
COMPUTABLE LINEAR ORDERS AND PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 605-623
- Print publication:
- June 2020
-
- Article
- Export citation
DOMINATION AND REGULARITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 19 January 2021, pp. 103-117
- Print publication:
- June 2020
-
- Article
- Export citation
SOME MODEL-THEORETIC RESULTS ON THE 3-VALUED PARACONSISTENT FIRST-ORDER LOGIC QCIORE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 09 December 2019, pp. 187-224
- Print publication:
- March 2021
-
- Article
- Export citation
Real closed valued fields with analytic structure
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 05 December 2019, pp. 249-261
-
- Article
-
- You have access
- Open access
- Export citation
Maximal hyperbolic towers and weight in the theory of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 479-498
- Print publication:
- May 2021
-
- Article
- Export citation
DEFINABLE SETS OF BERKOVICH CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1275-1339
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
THE MODAL LOGIC OF SET-THEORETIC POTENTIALISM AND THE POTENTIALIST MAXIMALITY PRINCIPLES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 04 October 2019, pp. 1-35
- Print publication:
- March 2022
-
- Article
- Export citation
Expansions of the Real Field by Canonical Products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 October 2019, pp. 506-521
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
THE FINITE BASIS PROBLEM FOR INVOLUTION SEMIGROUPS OF TRIANGULAR
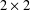 $2\times 2$ MATRICES
$2\times 2$ MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 88-104
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
CHARACTERIZING O-MINIMAL GROUPS IN TAME EXPANSIONS OF O-MINIMAL STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 July 2019, pp. 699-724
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
PROJECTIVE CLONE HOMOMORPHISMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 03 May 2019, pp. 148-161
- Print publication:
- March 2021
-
- Article
- Export citation
ENFORCEABLE OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 01 March 2019, pp. 31-63
- Print publication:
- January 2021
-
- Article
-
- You have access
- Export citation
RAMSEY GROWTH IN SOME NIP STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1-29
- Print publication:
- January 2021
-
- Article
- Export citation
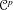 $\mathscr{C}^{p}$-parametrization in O-minimal Structures
$\mathscr{C}^{p}$-parametrization in O-minimal Structures
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 99-108
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
A Modular André–Oort Statement with Derivatives
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 323-365
-
- Article
- Export citation
Composite quasianalytic functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 1960-1973
- Print publication:
- September 2018
-
- Article
- Export citation
Model Completeness for the Real Field with the Weierstrass ℘ Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 811-823
-
- Article
- Export citation
STABILIZERS,
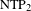 $\text{NTP}_{2}$ GROUPS WITH
$\text{NTP}_{2}$ GROUPS WITH  $\text{f}$-GENERICS, AND PRC FIELDS
$\text{f}$-GENERICS, AND PRC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 10 May 2018, pp. 821-853
- Print publication:
- May 2020
-
- Article
- Export citation
UNIVERSAL COVERS OF COMMUTATIVE FINITE MORLEY RANK GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 26 April 2018, pp. 767-799
- Print publication:
- May 2020
-
- Article
- Export citation