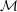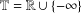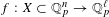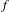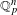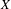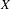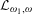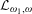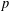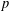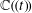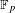Refine listing
Actions for selected content:
333 results in 03CXX
STABILIZERS,
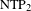 $\text{NTP}_{2}$ GROUPS WITH
$\text{NTP}_{2}$ GROUPS WITH  $\text{f}$-GENERICS, AND PRC FIELDS
$\text{f}$-GENERICS, AND PRC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 10 May 2018, pp. 821-853
- Print publication:
- May 2020
-
- Article
- Export citation
UNIVERSAL COVERS OF COMMUTATIVE FINITE MORLEY RANK GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 26 April 2018, pp. 767-799
- Print publication:
- May 2020
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
Generalized Euler characteristic in power-bounded T-convex valued fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 14 September 2017, pp. 2591-2642
- Print publication:
- December 2017
-
- Article
- Export citation
The Pila–Wilkie theorem for subanalytic families: a complex analytic approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2171-2194
- Print publication:
- October 2017
-
- Article
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 28 June 2016, e17
-
- Article
-
- You have access
- Open access
- Export citation
TWISTED GALOIS STRATIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 1-60
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
- Print publication:
- April 2018
-
- Article
- Export citation
THE FINITE BASIS PROBLEM FOR THE MONOID OF TWO-BY-TWO UPPER TRIANGULAR TROPICAL MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 54-64
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Rational Values of Weierstrass Zeta Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 945-958
-
- Article
- Export citation
A DEFINABLE
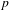 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
CATEGORICITY OF MODULAR AND SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1075-1101
- Print publication:
- November 2017
-
- Article
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
SOME PROPERTIES OF ANALYTIC DIFFERENCE VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 29 May 2015, pp. 447-499
- Print publication:
- June 2017
-
- Article
- Export citation
First-Order Convergence and Roots†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 24 February 2015, pp. 213-221
-
- Article
- Export citation
LOCAL INTERDEFINABILITY OF WEIERSTRASS ELLIPTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 24 November 2014, pp. 673-691
- Print publication:
- October 2016
-
- Article
- Export citation
COMPARING
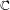 $\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
$\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 04 August 2014, pp. 71-84
- Print publication:
- January 2016
-
- Article
- Export citation
RIGIDITY OF CONTINUOUS QUOTIENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2014, pp. 1-28
- Print publication:
- January 2016
-
- Article
- Export citation
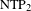

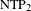
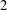
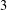

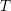
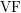
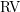
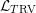
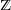
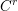
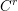
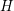
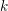
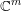
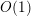
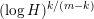


 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.