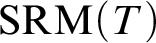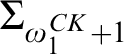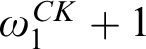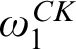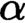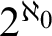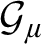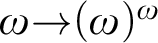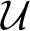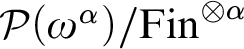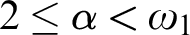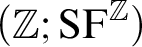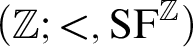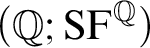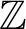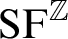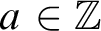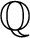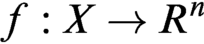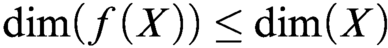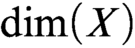Refine listing
Actions for selected content:
346 results in 03CXX
 $[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
$[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1632-1656
- Print publication:
- December 2021
-
- Article
- Export citation
CORES OVER RAMSEY STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 352-361
- Print publication:
- March 2021
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
SCOTT COMPLEXITY OF COUNTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1706-1720
- Print publication:
- December 2021
-
- Article
- Export citation
INQUISITIVE BISIMULATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 77-109
- Print publication:
- March 2021
-
- Article
- Export citation
THE KIM–PILLAY THEOREM FOR ABSTRACT ELEMENTARY CATEGORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1717-1741
- Print publication:
- December 2020
-
- Article
- Export citation
AROUND RUBIN’S “THEORIES OF LINEAR ORDER”
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1403-1426
- Print publication:
- December 2020
-
- Article
- Export citation
PSEUDO-FINITE SETS, PSEUDO-O-MINIMALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 577-599
- Print publication:
- June 2021
-
- Article
- Export citation
ELEMENTARY EQUIVALENCE THEOREM FOR PAC STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1467-1498
- Print publication:
- December 2020
-
- Article
- Export citation
COMPUTABILITY OF POLISH SPACES UP TO HOMEOMORPHISM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1664-1686
- Print publication:
- December 2020
-
- Article
- Export citation
STRONGLY MINIMAL STEINER SYSTEMS I: EXISTENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1486-1507
- Print publication:
- December 2021
-
- Article
- Export citation
CLASSES OF BARREN EXTENSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 178-209
- Print publication:
- March 2021
-
- Article
- Export citation
UNIFORM DEFINABILITY OF INTEGERS IN REDUCED INDECOMPOSABLE POLYNOMIAL RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1376-1402
- Print publication:
- December 2020
-
- Article
- Export citation
MODEL THEORY AND COMBINATORICS OF BANNED SEQUENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1-20
- Print publication:
- March 2022
-
- Article
- Export citation
THE ADDITIVE GROUPS OF
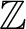 $\mathbb {Z}$ AND
$\mathbb {Z}$ AND 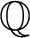 $\mathbb {Q}$ WITH PREDICATES FOR BEING SQUARE-FREE
$\mathbb {Q}$ WITH PREDICATES FOR BEING SQUARE-FREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1324-1349
- Print publication:
- December 2021
-
- Article
- Export citation
HOMOTOPY MODEL THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1301-1323
- Print publication:
- December 2021
-
- Article
- Export citation
DIMENSION INEQUALITY FOR A DEFINABLY COMPLETE UNIFORMLY LOCALLY O-MINIMAL STRUCTURE OF THE SECOND KIND
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1654-1663
- Print publication:
- December 2020
-
- Article
- Export citation
CONTINUOUS SENTENCES PRESERVED UNDER REDUCED PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 September 2020, pp. 649-681
- Print publication:
- June 2022
-
- Article
- Export citation
THE FUNDAMENTAL THEOREM OF CENTRAL ELEMENT THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1599-1606
- Print publication:
- December 2020
-
- Article
- Export citation
THE TREE OF TUPLES OF A STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 07 September 2020, pp. 21-46
- Print publication:
- March 2022
-
- Article
- Export citation