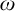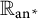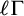Refine listing
Actions for selected content:
327 results in 03CXX
TRANSITIVITY, LOWNESS, AND RANKS IN NSOP
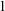 $_{1}$ THEORIES
$_{1}$ THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 919-946
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic differential equations are strongly minimal
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1387-1412
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Around Exponential-Algebraic Closedness
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 July 2023, p. 300
- Print publication:
- June 2023
-
- Article
-
- You have access
- Export citation
COFINALITY QUANTIFIERS IN ABSTRACT ELEMENTARY CLASSES AND BEYOND
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 26 May 2023, pp. 237-251
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLY COMPACT METRIC SPACES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 170-263
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMI-EQUATIONAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 10 May 2023, pp. 391-422
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHAT MODEL COMPANIONSHIP CAN SAY ABOUT THE CONTINUUM PROBLEM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 546-585
- Print publication:
- June 2024
-
- Article
- Export citation
COMPUTABLE PRESENTATIONS OF C*-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1313-1338
- Print publication:
- September 2024
-
- Article
- Export citation
INFINITARY LOGIC HAS NO EXPRESSIVE EFFICIENCY OVER FINITARY LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1817-1834
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REMARKS ON CONVERGENCE OF MORLEY SEQUENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1339-1357
- Print publication:
- September 2024
-
- Article
- Export citation
THE EMBEDDING PROPERTY FOR SORTED PROFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1005-1037
- Print publication:
- September 2023
-
- Article
- Export citation
ON COHESIVE POWERS OF LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 947-1004
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THEORIES WITH DISTAL SHELAH EXPANSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 1323-1333
- Print publication:
- December 2023
-
- Article
- Export citation
WHICH CLASSES OF STRUCTURES ARE BOTH PSEUDO-ELEMENTARY AND DEFINABLE BY AN INFINITARY SENTENCE?
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1-18
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multisummability for generalized power series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 458-494
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SATURATED MODELS FOR THE WORKING MODEL THEORIST
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 163-169
- Print publication:
- June 2023
-
- Article
- Export citation
ELIMINATION OF IMAGINARIES IN ORDERED ABELIAN GROUPS WITH BOUNDED REGULAR RANK
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 06 February 2023, pp. 1639-1654
- Print publication:
- December 2023
-
- Article
- Export citation
MAXIMALITY OF LOGIC WITHOUT IDENTITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 January 2023, pp. 147-162
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SELF-EMBEDDINGS OF MODELS OF ARITHMETIC; FIXED POINTS, SMALL SUBMODELS, AND EXTENDABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2022, pp. 1044-1066
- Print publication:
- September 2024
-
- Article
- Export citation
ISOMORPHISM OF LOCALLY COMPACT POLISH METRIC STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 19 December 2022, pp. 646-664
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation