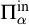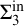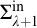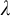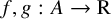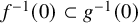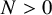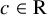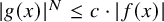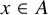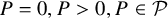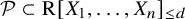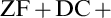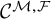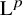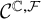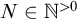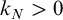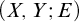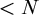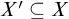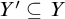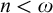Refine listing
Actions for selected content:
345 results in 03CXX
Structural convergence and algebraic roots
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 392-400
-
- Article
- Export citation
On ordinary differentially large fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABLE HENSELIAN VALUATIONS IN POSITIVE RESIDUE CHARACTERISTIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COMPACTNESS OF GÖDEL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-10
-
- Article
- Export citation
ON THE EXPRESSIVE POWER OF INQUISITIVE EPISTEMIC LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SATISFACTION CLASSES WITH APPROXIMATE DISJUNCTIVE CORRECTNESS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 545-562
- Print publication:
- June 2025
-
- Article
- Export citation
Quasiminimality of complex powers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e123
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCRETE SETS DEFINABLE IN STRONG EXPANSIONS OF ORDERED ABELIAN GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 423-459
- Print publication:
- March 2025
-
- Article
- Export citation
SCOTT SENTENCE COMPLEXITIES OF LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-30
-
- Article
- Export citation
FINITE-DIMENSIONAL DIFFERENTIAL-ALGEBRAIC PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 603-626
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved effective Łojasiewicz inequality and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 December 2024, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ULTRAPRODUCTS, THE SPECTRAL THEOREM AND RIGGED HILBERT SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 17 December 2024, pp. 1397-1429
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New Results in Model Theory and Set Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, pp. 543-544
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Parametric Fourier and Mellin transforms of power-constructible functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 November 2024, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE STRONG ERDŐS–HAJNAL PROPERTY FOR GRAPHS WITH BOUNDED VC-MINIMAL COMPLEXITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERIC DERIVATIONS ON ALGEBRAICALLY BOUNDED STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-27
-
- Article
- Export citation
THE GROUP CONFIGURATION THEOREM FOR GENERICALLY STABLE TYPES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 681-724
- Print publication:
- June 2025
-
- Article
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRICTLY n-FINITE VARIETIES OF HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GROUPS AND FIELDS DEFINABLE IN
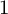 $1$-H-MINIMAL FIELDS
$1$-H-MINIMAL FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 203-248
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation