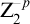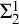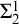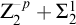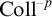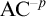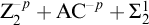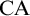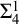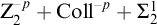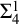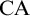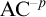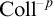Refine listing
Actions for selected content:
345 results in 03CXX
Echeloned Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTRACTING ENDOMORPHISMS OF VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 2047-2106
- Print publication:
- September 2025
-
- Article
- Export citation
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
DP AND OTHER MINIMALITIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-30
-
- Article
- Export citation
MODEL THEORY OF DIFFERENTIAL-HENSELIAN PRE-H-FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENRICHED CONCEPTS OF REGULAR LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linearity of compact R-analytic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 787-794
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 194-200
- Print publication:
- August 2025
-
- Article
- Export citation
UNIVERSALITY PROPERTIES OF FORCING
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 March 2025, pp. 1-19
-
- Article
- Export citation
THE KAUFMANN–CLOTE QUESTION ON END EXTENSIONS OF MODELS OF ARITHMETIC AND THE WEAK REGULARITY PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A MODULAR BISIMULATION CHARACTERISATION FOR FRAGMENTS OF HYBRID LOGIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 590-618
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE NON-EXISTENCE OF PRIME MODELS OF THEORIES OF PSEUDO-FINITE FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 52-67
- Print publication:
- March 2025
-
- Article
- Export citation
DIMENSION AND MEASURE IN PSEUDOFINITE H-STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 68-104
- Print publication:
- March 2025
-
- Article
- Export citation
TORSION-FREE ABELIAN GROUPS OF FINITE RANK AND FIELDS OF FINITE TRANSCENDENCE DEGREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 February 2025, pp. 1-30
-
- Article
- Export citation
ASYMPTOTIC TRUTH-VALUE LAWS IN MANY-VALUED LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARAMETER-FREE SCHEMES IN SECOND-ORDER ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-19
-
- Article
- Export citation
Rich representations and superrigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2249-2272
- Print publication:
- August 2025
-
- Article
- Export citation
OMEGA-CATEGORICAL PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LATTICE PROBLEM FOR MODELS OF
 $\mathsf {PA}$
$\mathsf {PA}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-28
-
- Article
- Export citation
FEFERMAN’S COMPLETENESS THEOREM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 462-487
- Print publication:
- September 2025
-
- Article
- Export citation