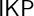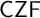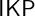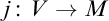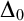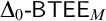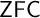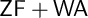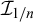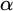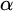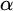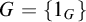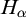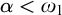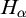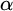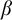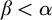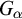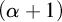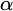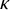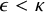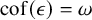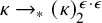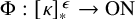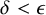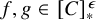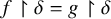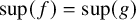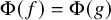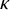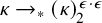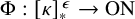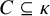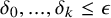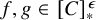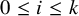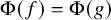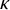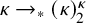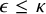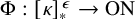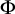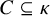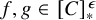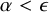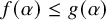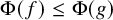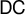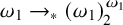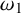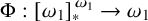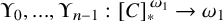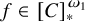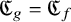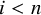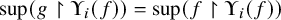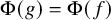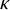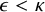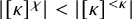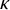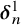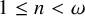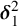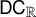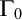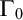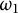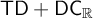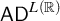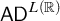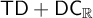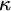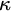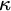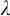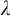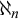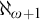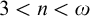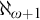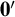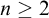Refine listing
Actions for selected content:
374 results in 03EXX
VERY LARGE SET AXIOMS OVER CONSTRUCTIVE SET THEORIES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 455-535
- Print publication:
- December 2024
-
- Article
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
Almost Everywhere Behavior of Functions According to Partition Measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINCARÉ–WEYL’S PREDICATIVITY: GOING BEYOND
 $\Gamma _{0}$
$\Gamma _{0}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 41-91
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1798-1816
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel reducibility of equivalence relations on
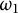 $\omega _1$
$\omega _1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 687-700
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON COMPACTNESS OF WEAK SQUARE AT SINGULARS OF UNCOUNTABLE COFINALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 January 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTE ON
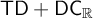 $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING 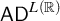 $\mathsf {AD}^{L(\mathbb {R})}$
$\mathsf {AD}^{L(\mathbb {R})}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 211-217
- Print publication:
- March 2024
-
- Article
- Export citation
PARTITION OF LARGE SUBSETS OF SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-6
-
- Article
- Export citation
STRONG MEASURE ZERO SETS ON
 $2^\kappa $ FOR
$2^\kappa $ FOR  $\kappa $ INACCESSIBLE
$\kappa $ INACCESSIBLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1277-1307
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEBESGUE MEASURE ZERO MODULO IDEALS ON THE NATURAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 29 December 2023, pp. 1098-1128
- Print publication:
- September 2025
-
- Article
- Export citation
THE STRONG AND SUPER TREE PROPERTIES AT SUCCESSORS OF SINGULAR CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1251-1283
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARACONSISTENT AND PARACOMPLETE ZERMELO–FRAENKEL SET THEORY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 965-995
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A BOREL MAXIMAL COFINITARY GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 11 December 2023, pp. 808-821
- Print publication:
- June 2025
-
- Article
- Export citation
DEGREE SPECTRA OF HOMEOMORPHISM TYPE OF COMPACT POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-32
-
- Article
- Export citation
MORE ON BLURRY HOD
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 07 December 2023, pp. 822-853
- Print publication:
- June 2025
-
- Article
- Export citation
DIVERGENT MODELS WITH THE FAILURE OF THE CONTINUUM HYPOTHESIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 December 2023, pp. 1-11
-
- Article
- Export citation
Weak Indestructibility and Reflection
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2024, p. 663
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1919-1957
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation