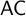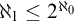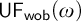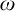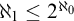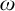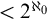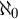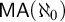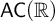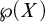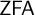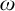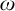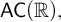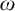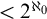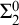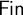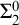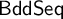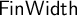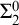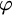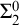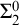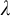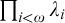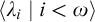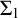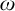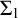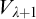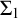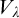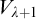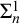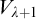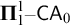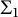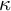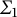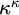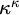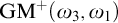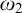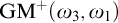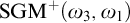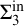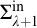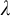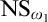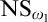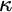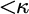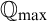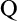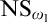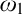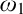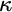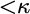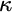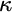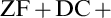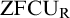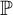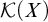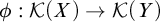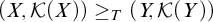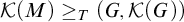Refine listing
Actions for selected content:
374 results in 03EXX
ON FREE ULTRAFILTERS ON
 $\omega $ WITH WELL-ORDERABLE BASES IN
$\omega $ WITH WELL-ORDERABLE BASES IN  $\mathsf {ZF}$
$\mathsf {ZF}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MANY-ONE REDUCIBILITY WITH REALIZABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-39
-
- Article
- Export citation
DESCRIPTIVE PROPERTIES OF I2-EMBEDDINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WEIHRAUCH LATTICE AT THE LEVEL OF
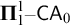 $\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM
$\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 752-790
- Print publication:
- June 2025
-
- Article
- Export citation
On
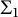 $\Sigma _1$-definable closed unbounded sets
$\Sigma _1$-definable closed unbounded sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALIZED TOWER SPECTRA
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 January 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON INDESTRUCTIBLE STRONGLY GUESSING MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-27
-
- Article
- Export citation
THE ERDŐS–HAJNAL PROBLEM LIST
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 418-461
- Print publication:
- September 2025
-
- Article
- Export citation
THE GENERIC MULTIVERSE IS NOT GOING AWAY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 671-703
- Print publication:
- September 2025
-
- Article
- Export citation
SCOTT SENTENCE COMPLEXITIES OF LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-30
-
- Article
- Export citation
Infinite dimensional sequential compactness: Sequential compactness based on barriers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 2083-2110
- Print publication:
- December 2025
-
- Article
- Export citation
Generic properties of topological groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A ONE-PAGE PROOF OF A THEOREM OF BELEZNAY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, pp. 536-537
- Print publication:
- December 2024
-
- Article
- Export citation
THE UNIQUENESS OF ELEMENTARY EMBEDDINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1430-1454
- Print publication:
- December 2024
-
- Article
- Export citation
Forcing “
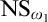 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 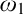 $\omega _1$-Dense” from Large Cardinals
$\omega _1$-Dense” from Large Cardinals
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, p. 544
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
New Results in Model Theory and Set Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, pp. 543-544
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
AXIOMATIZATION AND FORCING IN SET THEORY WITH URELEMENTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-27
-
- Article
- Export citation
BOREL LINE GRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTABLE SPACES, REALCOMPACTNESS, AND THE PSEUDOINTERSECTION NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
- Export citation