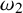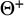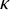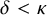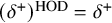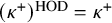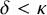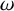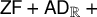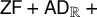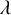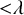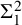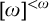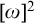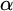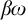Refine listing
Actions for selected content:
374 results in 03EXX
ON THE CATEGORICITY OF COMPLETE SECOND-ORDER THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-23
-
- Article
- Export citation
OF SHEEP AND WOLVES: EQUIVALENCE AND DISAGREEMENT IN SET THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 26 August 2025, pp. 619-685
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON WINNING STRATEGIES FOR
 $F_\sigma $ GAMES
$F_\sigma $ GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-15
-
- Article
- Export citation
THE WEAK EXTENSION PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-11
-
- Article
- Export citation
SET-THEORETIC BICONTEXTUALISM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 22 August 2025, pp. 826-858
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABSTRACTION PRINCIPLES AND THE SIZE OF REALITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 19 August 2025, pp. 812-825
- Print publication:
- September 2025
-
- Article
- Export citation
MEASURABLE DOMATIC PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-25
-
- Article
- Export citation
UNIFORMITY NUMBERS OF THE NULL-ADDITIVE AND MEAGER-ADDITIVE IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-37
-
- Article
- Export citation
SEPARATING SUBVERSION FORCING AXIOMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 30 July 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\textsf {AD}^{+}$ implies
$\textsf {AD}^{+}$ implies  $ \omega _{1}$ is a club
$ \omega _{1}$ is a club  $ \Theta $-Berkeley cardinal
$ \Theta $-Berkeley cardinal
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 July 2025, e126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compactness phenomena in HOD
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ÉTALE STRUCTURES AND THE JOYAL–TIERNEY REPRESENTATION THEOREM IN COUNTABLE MODEL THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 July 2025, pp. 1-52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A model of the Axiom of Determinacy in which every set of reals is universally Baire
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 June 2025, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PRODUCTS OF ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-17
-
- Article
- Export citation
CORONA RIGIDITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 195-287
- Print publication:
- June 2025
-
- Article
- Export citation
Density of monochromatic infinite subgraphs II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A counterexample regarding an equivalence relation on a product space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1262-1266
- Print publication:
- December 2025
-
- Article
- Export citation
The nonabelian product modulo sum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1069-1109
-
- Article
- Export citation
PFA AND THE DEFINABILITY OF THE NONSTATIONARY IDEAL
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-8
-
- Article
- Export citation
HIGH DIMENSIONAL COUNTABLE COMPACTNESS AND ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-21
-
- Article
- Export citation


















































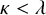
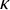

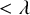


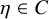


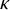
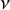
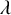




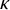

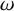



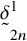 ’s are
’s are