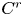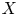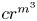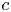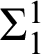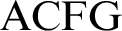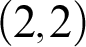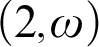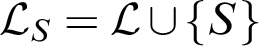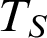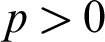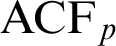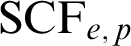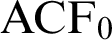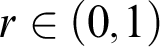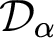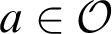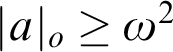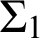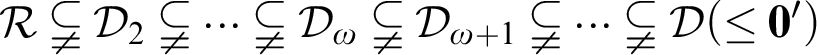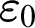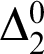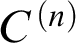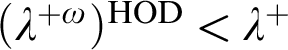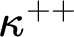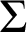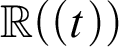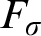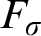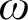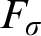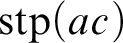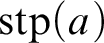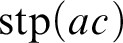Refine listing
Actions for selected content:
1095 results in 03xxx
Smooth parameterizations of power-subanalytic sets and compositions of Gevrey functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 532-554
-
- Article
- Export citation
GOODSTEIN SEQUENCES BASED ON A PARAMETRIZED ACKERMANN–PÉTER FUNCTION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 168-186
- Print publication:
- June 2021
-
- Article
- Export citation
FORKING, IMAGINARIES, AND OTHER FEATURES OF
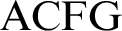 $\text {ACFG}$
$\text {ACFG}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 669-700
- Print publication:
- June 2021
-
- Article
- Export citation
The Structure of d.r.e. Degrees
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 218-219
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Expansions and Neostability in Model Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 216-217
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Intrinsic density, asymptotic computability, and stochasticity
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, p. 220
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Necessitism, Contingentism, and Theory Equivalence
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 217-218
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Pseudofinite Structures and Counting Dimensions
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, p. 223
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
On Transfinite Levels of the Ershov Hierarchy
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 220-221
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Results on Martin’s Conjecture
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 219-220
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Contributions to the Theory of Large Cardinals through the Method of Forcing
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 221-222
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
From Generative Linguistics to Categorial Grammars: Overt Subjects in Control Infinitives
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, p. 215
- Print publication:
- June 2021
-
- Article
-
- You have access
- HTML
- Export citation
FORCING AXIOMS, APPROACHABILITY, AND STATIONARY SET REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 20 October 2021, pp. 499-530
- Print publication:
- June 2021
-
- Article
- Export citation
Transfer Principles in Henselian Valued Fields
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 222-223
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Model Theory in a Paraconsistent Environment
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, p. 216
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
BOUNDED-ANALYTIC SEQUENT CALCULI AND EMBEDDINGS FOR HYPERSEQUENT LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2021, pp. 635-668
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TUKEY ORDER AMONG
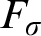 $F_{\sigma }$ IDEALS
$F_{\sigma }$ IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 855-870
- Print publication:
- June 2021
-
- Article
- Export citation
CLOSURE PROPERTIES OF MEASURABLE ULTRAPOWERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 762-784
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE RELATIVIZED LASCAR GROUPS, TYPE-AMALGAMATION, AND ALGEBRAICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 531-557
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEVEL THEORY, PART 1: AXIOMATIZING THE BARE IDEA OF A CUMULATIVE HIERARCHY OF SETS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 436-460
- Print publication:
- December 2021
-
- Article
- Export citation