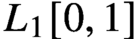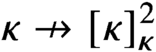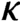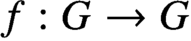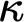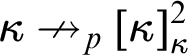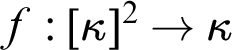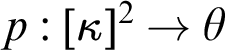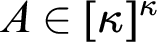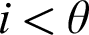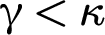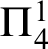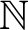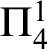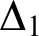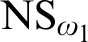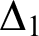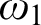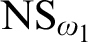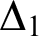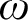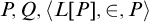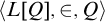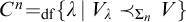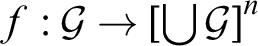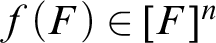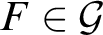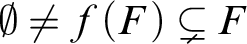Refine listing
Actions for selected content:
1095 results in 03xxx
Uniformly factoring weakly compact operators and parametrised dualisation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 March 2021, e22
-
- Article
-
- You have access
- Open access
- Export citation
CARNAP’S PROBLEM FOR MODAL LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 March 2021, pp. 578-602
- Print publication:
- June 2023
-
- Article
- Export citation
Transformations of the transfinite plane
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 March 2021, e16
-
- Article
-
- You have access
- Open access
- Export citation
REDUCTION TECHNIQUES FOR PROVING DECIDABILITY IN LOGICS AND THEIR MEET–COMBINATION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 39-66
- Print publication:
- March 2021
-
- Article
- Export citation
BOLZANO’S MATHEMATICAL INFINITE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 22 February 2021, pp. 59-113
- Print publication:
- March 2023
-
- Article
- Export citation
FREGE’S THEORY OF REAL NUMBERS: A CONSISTENT RENDERING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 624-667
- Print publication:
- September 2022
-
- Article
- Export citation
STRONG COLORINGS OVER PARTITIONS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 22 February 2021, pp. 67-90
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRIORITY MERGE AND INTERSECTION MODALITIES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 165-196
- Print publication:
- March 2022
-
- Article
- Export citation
GÖDEL ON MANY-VALUED LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 22 February 2021, pp. 655-671
- Print publication:
- September 2023
-
- Article
- Export citation
THE SEMANTIC FOUNDATIONS OF PHILOSOPHICAL ANALYSIS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 February 2021, pp. 603-623
- Print publication:
- June 2023
-
- Article
- Export citation
WELL ORDERING PRINCIPLES AND
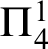 ${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 February 2021, pp. 709-745
- Print publication:
- June 2021
-
- Article
- Export citation
NS SATURATED AND
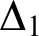 ${\Delta }_{1}$-DEFINABLE
${\Delta }_{1}$-DEFINABLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 16 February 2021, pp. 25-59
- Print publication:
- March 2021
-
- Article
- Export citation
COMBINATORICS OF ULTRAFILTERS ON COHEN AND RANDOM ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 109-126
- Print publication:
- March 2022
-
- Article
- Export citation
RAMSEY’S COHEIRS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 377-391
- Print publication:
- March 2022
-
- Article
- Export citation
THICKET DENSITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 110-127
- Print publication:
- March 2021
-
- Article
- Export citation
ONE DIMENSIONAL GROUPS DEFINABLE IN THE p-ADIC NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 801-816
- Print publication:
- June 2021
-
- Article
- Export citation
RECURRENCE AND THE EXISTENCE OF INVARIANT MEASURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 60-76
- Print publication:
- March 2021
-
- Article
- Export citation
SEPARATING DIAGONAL STATIONARY REFLECTION PRINCIPLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 262-292
- Print publication:
- March 2021
-
- Article
- Export citation
CLOSED AND UNBOUNDED CLASSES AND THE HÄRTIG QUANTIFIER MODEL
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 564-584
- Print publication:
- June 2022
-
- Article
- Export citation
THE RELATION BETWEEN TWO DIMINISHED CHOICE PRINCIPLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 415-432
- Print publication:
- March 2021
-
- Article
- Export citation