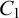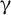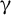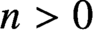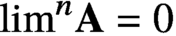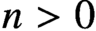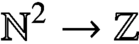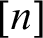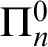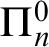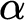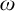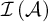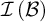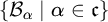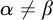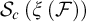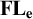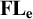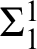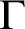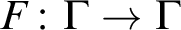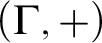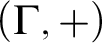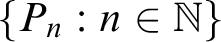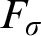Refine listing
Actions for selected content:
1095 results in 03xxx
INTERPRETATION, LOGIC AND PHILOSOPHY: JEAN NICOD’S GEOMETRY IN THE SENSIBLE WORLD
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 1080-1109
- Print publication:
- December 2023
-
- Article
- Export citation
LOGICS OF FORMAL INCONSISTENCY ENRICHED WITH REPLACEMENT: AN ALGEBRAIC AND MODAL ACCOUNT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 771-806
- Print publication:
- September 2022
-
- Article
- Export citation
Unique ergodicity of the automorphism group of the semigeneric directed graph
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 28 June 2021, pp. 2561-2574
- Print publication:
- August 2022
-
- Article
- Export citation
NULL SETS AND COMBINATORIAL COVERING PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 1231-1242
- Print publication:
- September 2022
-
- Article
- Export citation
Simultaneously vanishing higher derived limits
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 June 2021, e4
-
- Article
-
- You have access
- Open access
- Export citation
THE COPERNICAN MULTIVERSE OF SETS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 1033-1069
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEAK CANONICAL BASES IN NSOP
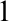 $_1$ THEORIES
$_1$ THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 June 2021, pp. 1259-1281
- Print publication:
- September 2021
-
- Article
- Export citation
PRENEX NORMAL FORM THEOREMS IN SEMI-CLASSICAL ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 June 2021, pp. 1124-1153
- Print publication:
- September 2021
-
- Article
- Export citation
THE POSET OF ALL LOGICS II: LEIBNIZ CLASSES AND HIERARCHY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 June 2021, pp. 324-362
- Print publication:
- March 2023
-
- Article
- Export citation
ORDINAL ANALYSIS OF PARTIAL COMBINATORY ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1154-1188
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MÜNCHHAUSEN PROVABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1006-1034
- Print publication:
- September 2021
-
- Article
- Export citation
FIBRED ALGEBRAIC SEMANTICS FOR A VARIETY OF NON-CLASSICAL FIRST-ORDER LOGICS AND TOPOLOGICAL LOGICAL TRANSLATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1189-1213
- Print publication:
- September 2021
-
- Article
- Export citation
MORE ON FRÉCHET–URYSOHN IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 829-851
- Print publication:
- June 2022
-
- Article
- Export citation
MOST SIMPLE EXTENSIONS OF
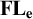 $\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
$\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1156-1200
- Print publication:
- September 2022
-
- Article
- Export citation
THE POSET OF ALL LOGICS I: INTERPRETATIONS AND LATTICE STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 935-964
- Print publication:
- September 2021
-
- Article
- Export citation
A COMPARISON OF VARIOUS ANALYTIC CHOICE PRINCIPLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1452-1485
- Print publication:
- December 2021
-
- Article
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
- Print publication:
- September 2021
-
- Article
- Export citation
CONTRIBUTIONS TO THE THEORY OF F-AUTOMATIC SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 127-158
- Print publication:
- March 2022
-
- Article
- Export citation
MODELS OF MARTIN-LÖF TYPE THEORY FROM ALGEBRAIC WEAK FACTORISATION SYSTEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 June 2021, pp. 242-289
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTABLY PERFECTLY MEAGER SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 1214-1227
- Print publication:
- September 2021
-
- Article
- Export citation