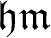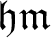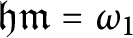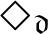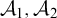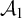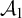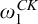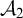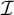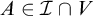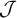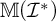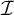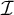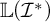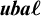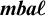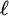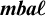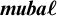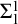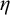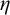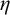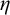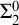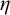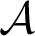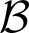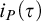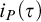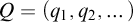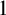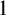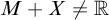Refine listing
Actions for selected content:
1095 results in 03xxx
The ultrafilter number and
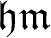 $\mathfrak {hm}$
$\mathfrak {hm}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 03 November 2021, pp. 494-530
- Print publication:
- April 2023
-
- Article
- Export citation
FIRST-ORDER AXIOMATISATIONS OF REPRESENTABLE RELATION ALGEBRAS NEED FORMULAS OF UNBOUNDED QUANTIFIER DEPTH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1283-1300
- Print publication:
- September 2022
-
- Article
- Export citation
HIGHER MILLER FORCING MAY COLLAPSE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1721-1744
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURAL CONSIDERATIONS OF RAMSEY ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1677-1692
- Print publication:
- December 2022
-
- Article
- Export citation
ALMOST DISJOINT AND MAD FAMILIES IN VECTOR SPACES AND CHOICE PRINCIPLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1093-1110
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COPYING ONE OF A PAIR OF STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1201-1214
- Print publication:
- September 2022
-
- Article
- Export citation
FINITE RELATION ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 October 2021, pp. 874-888
- Print publication:
- June 2023
-
- Article
- Export citation
LOCALLY O-MINIMAL STRUCTURES WITH TAME TOPOLOGICAL PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 219-241
- Print publication:
- March 2023
-
- Article
- Export citation
WAYS OF DESTRUCTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 938-966
- Print publication:
- September 2022
-
- Article
- Export citation
MODAL OPERATORS ON RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1322-1348
- Print publication:
- December 2022
-
- Article
- Export citation
DEGREE SPECTRA OF ANALYTIC COMPLETE EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1663-1676
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms yield upper bounds in differential algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 29-51
- Print publication:
- February 2023
-
- Article
- Export citation
GRZEGORCZYK POINTS AND FILTERS IN BOOLEAN CONTACT ALGEBRAS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 September 2021, pp. 509-528
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CHARACTERIZATION OF THE STRONGLY
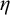 $\eta $-REPRESENTABLE MANY-ONE DEGREES
$\eta $-REPRESENTABLE MANY-ONE DEGREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1631-1642
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGREES OF RANDOMIZED COMPUTABILITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 27-70
- Print publication:
- March 2022
-
- Article
- Export citation
ACKERMANN’S FUNCTION IN ITERATIVE FORM: A PROOF ASSISTANT EXPERIMENT
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 27 September 2021, pp. 426-435
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFORMATION IN PROPOSITIONAL PROOFS AND ALGORITHMIC PROOF SEARCH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 852-869
- Print publication:
- June 2022
-
- Article
- Export citation
DESCRIPTIVE COMPLEXITY IN CANTOR SERIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1023-1045
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MOST(?) THEORIES HAVE BOREL COMPLETE REDUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 September 2021, pp. 418-426
- Print publication:
- March 2023
-
- Article
- Export citation
MEAGER-ADDITIVE SETS IN TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1046-1064
- Print publication:
- September 2022
-
- Article
- Export citation