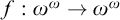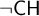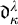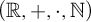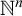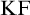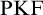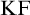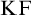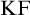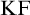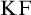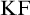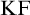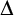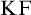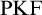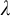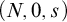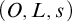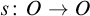Refine listing
Actions for selected content:
1095 results in 03xxx
HIGHER DIMENSIONAL CARDINAL CHARACTERISTICS FOR SETS OF FUNCTIONS II
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 1421-1442
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SIMPLE SEQUENT SYSTEM FOR MINIMALLY INCONSISTENT LP
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2022, pp. 1296-1311
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TOWARDS THE INEVITABILITY OF NON-CLASSICAL PROBABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 1053-1079
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EUCLIDEAN NUMBERS AND NUMEROSITIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 February 2022, pp. 112-146
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INITIAL SEGMENTS OF THE DEGREES OF CEERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1260-1282
- Print publication:
- September 2022
-
- Article
- Export citation
Bounds for a nonlinear ergodic theorem for Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1570-1593
- Print publication:
- May 2023
-
- Article
- Export citation
CONNECTEDNESS IN STRUCTURES ON THE REAL NUMBERS: O-MINIMALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1243-1259
- Print publication:
- September 2022
-
- Article
- Export citation
MUTUAL INTERPRETABILITY OF WEAK ESSENTIALLY UNDECIDABLE THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1374-1395
- Print publication:
- December 2022
-
- Article
- Export citation
TREES AND STATIONARY REFLECTION AT DOUBLE SUCCESSORS OF REGULAR CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 14 February 2022, pp. 780-810
- Print publication:
- June 2023
-
- Article
- Export citation
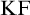 $\mathrm {KF}$,
$\mathrm {KF}$, 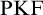 $\mathrm {PKF}$, AND REINHARDT’S PROGRAM
$\mathrm {PKF}$, AND REINHARDT’S PROGRAM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 33-58
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PLURAL ANCESTRAL LOGIC AS THE LOGIC OF ARITHMETIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 February 2022, pp. 305-342
- Print publication:
- June 2024
-
- Article
- Export citation
TAKING REINHARDT’S POWER AWAY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 1643-1662
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBCOMPACT CARDINALS, TYPE OMISSION, AND LADDER SYSTEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1111-1129
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLETE INTUITIONISTIC TEMPORAL LOGICS FOR TOPOLOGICAL DYNAMICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 February 2022, pp. 995-1022
- Print publication:
- September 2022
-
- Article
- Export citation
MEREOLOGICAL BIMODAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 823-858
- Print publication:
- December 2022
-
- Article
- Export citation
A SUBSTRUCTURAL GENTZEN CALCULUS FOR ORTHOMODULAR QUANTUM LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 1177-1198
- Print publication:
- December 2023
-
- Article
- Export citation
CONSTRUCTING WADGE CLASSES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 207-257
- Print publication:
- June 2022
-
- Article
- Export citation
A DEDEKIND-STYLE AXIOMATIZATION AND THE CORRESPONDING UNIVERSAL PROPERTY OF AN ORDINAL NUMBER SYSTEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1396-1418
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOOLEAN TYPES IN DEPENDENT THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1349-1373
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation