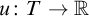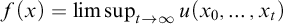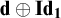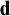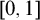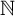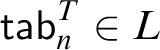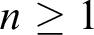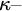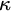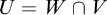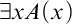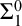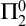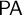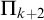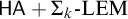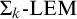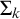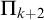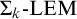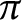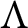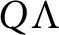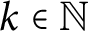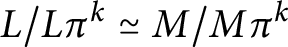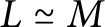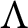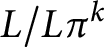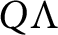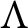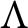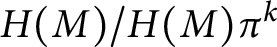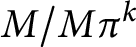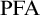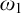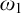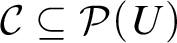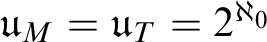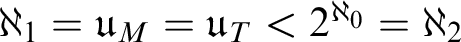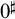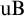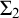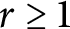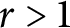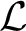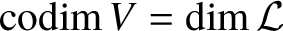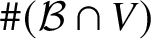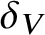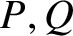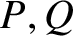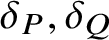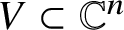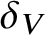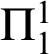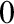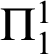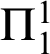Refine listing
Actions for selected content:
1095 results in 03xxx
GAMES CHARACTERIZING LIMSUP FUNCTIONS AND BAIRE CLASS 1 FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1459-1473
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STRUCTURE OF COMPUTABLE REDUCIBILITY ON EQUIVALENCE RELATIONS OF NATURAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 April 2022, pp. 1038-1063
- Print publication:
- September 2023
-
- Article
- Export citation
HUME’S PRINCIPLE, BAD COMPANY, AND THE AXIOM OF CHOICE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 08 April 2022, pp. 1158-1176
- Print publication:
- December 2023
-
- Article
- Export citation
ON THE UNCOUNTABILITY OF
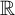 ${\mathbb R}$
${\mathbb R}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 07 April 2022, pp. 1474-1521
- Print publication:
- December 2022
-
- Article
- Export citation
TABULARITY AND POST-COMPLETENESS IN TENSE LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 April 2022, pp. 475-492
- Print publication:
- June 2024
-
- Article
- Export citation
AN AXIOMATIC APPROACH TO FORCING IN A GENERAL SETTING
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 April 2022, pp. 427-450
- Print publication:
- September 2022
-
- Article
- Export citation
ON RESTRICTIONS OF ULTRAFILTERS FROM GENERIC EXTENSIONS TO GROUND MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 169-190
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COLLAPSE OF THE HILBERT PROGRAM: A VARIATION ON THE GÖDELIAN THEME
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 413-426
- Print publication:
- September 2022
-
- Article
- Export citation
CONSERVATION THEOREMS ON SEMI-CLASSICAL ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 March 2022, pp. 1469-1496
- Print publication:
- December 2023
-
- Article
- Export citation
Maranda’s theorem for pure-injective modules and duality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 March 2022, pp. 581-607
- Print publication:
- April 2023
-
- Article
- Export citation
SPECIALISING TREES WITH SMALL APPROXIMATIONS I
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 March 2022, pp. 640-663
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORCING CONSTRUCTIONS AND COUNTABLE BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 873-893
- Print publication:
- September 2022
-
- Article
- Export citation
A GENERALIZED CANTOR THEOREM IN
 $\mathsf {ZF}$
$\mathsf {ZF}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 March 2022, pp. 204-210
- Print publication:
- March 2024
-
- Article
- Export citation
SET THEORY AND A MODEL OF THE MIND IN PSYCHOLOGY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1233-1259
- Print publication:
- December 2023
-
- Article
- Export citation
MODEL THEORY OF FIELDS WITH FINITE GROUP SCHEME ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1443-1468
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE CONSISTENCY STRENGTH OF THE PERFECT SET PROPERTY FOR UNIVERSALLY BAIRE SETS OF REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 508-526
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a topological Ramsey theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 156-165
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Point counting for foliations over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THEOREMS OF HYPERARITHMETIC ANALYSIS AND ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 31 March 2022, pp. 133-149
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The spectrum of a localic semiring
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 647-668
- Print publication:
- November 2022
-
- Article
- Export citation