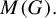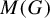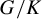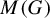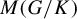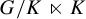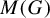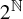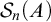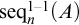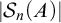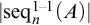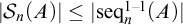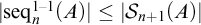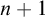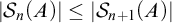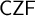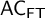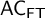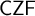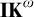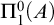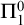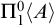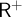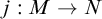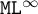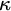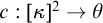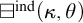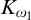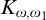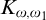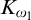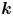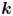Refine listing
Actions for selected content:
1095 results in 03xxx
Universal minimal flows of extensions of and by compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 04 August 2022, pp. 2538-2548
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 664-696
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PERMUTATIONS WITH n NON-FIXED POINTS AND THE SEQUENCES WITH LENGTH n OF A SET
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 July 2022, pp. 1067-1076
- Print publication:
- September 2024
-
- Article
- Export citation
AFFINE LOGIC FOR CONSTRUCTIVE MATHEMATICS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 July 2022, pp. 327-386
- Print publication:
- September 2022
-
- Article
- Export citation
EXTENSIONAL REALIZABILITY AND CHOICE FOR DEPENDENT TYPES IN INTUITIONISTIC SET THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 20 July 2022, pp. 1138-1169
- Print publication:
- September 2023
-
- Article
- Export citation
ON ZARDINI’S RULES FOR MULTIPLICATIVE QUANTIFICATION AS THE SOURCE OF CONTRA(DI)CTIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 July 2022, pp. 1110-1119
- Print publication:
- December 2023
-
- Article
- Export citation
PA RELATIVE TO AN ENUMERATION ORACLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 18 July 2022, pp. 1497-1525
- Print publication:
- December 2023
-
- Article
- Export citation
COLLECTION FRAMES FOR DISTRIBUTIVE SUBSTRUCTURAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 1120-1157
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EMBEDDINGS INTO OUTER MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 1301-1321
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING TO INFINITY: GRADED MODAL LOGIC WITH AN INFINITY DIAMOND
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1-35
- Print publication:
- March 2024
-
- Article
- Export citation
THE FIRST-ORDER LOGIC OF CZF IS INTUITIONISTIC FIRST-ORDER LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 08 July 2022, pp. 308-330
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROBABILISTIC ENTAILMENT ON FIRST ORDER LANGUAGES AND REASONING WITH INCONSISTENCIES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 351-368
- Print publication:
- June 2023
-
- Article
- Export citation
KNASTER AND FRIENDS III: SUBADDITIVE COLORINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 1230-1280
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAKER–BREAKER GAMES ON
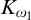 $ K_{\omega _1}$ AND
$ K_{\omega _1}$ AND 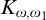 $K_{\omega ,\omega _1}$
$K_{\omega ,\omega _1}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 697-703
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF GALOIS ACTIONS OF TORSION ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 2943-2985
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALGEBRAIC EXPANSIONS OF LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 74-92
- Print publication:
- March 2023
-
- Article
- Export citation
CONTINUOUS LOGIC AND BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 1725-1752
- Print publication:
- December 2023
-
- Article
- Export citation
An uncountable Furstenberg–Zimmer structure theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 2404-2436
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting closed asymptotic couples
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 20 June 2022, pp. 530-555
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ADDITIVE COVERS AND THE CANONICAL BASE PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 118-144
- Print publication:
- March 2023
-
- Article
- Export citation