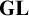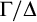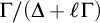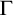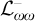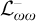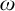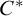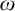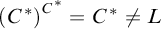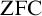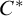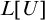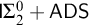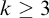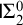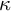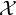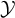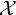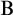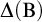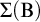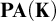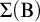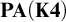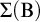Refine listing
Actions for selected content:
1095 results in 03xxx
COMPLETENESS OF THE GÖDEL–LÖB PROVABILITY LOGIC FOR THE FILTER SEQUENCE OF NORMAL MEASURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 February 2023, pp. 163-174
- Print publication:
- March 2024
-
- Article
- Export citation
INTUITIONISTIC SAHLQVIST THEORY FOR DEDUCTIVE SYSTEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 February 2023, pp. 1522-1580
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SATURATED MODELS FOR THE WORKING MODEL THEORIST
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 163-169
- Print publication:
- June 2023
-
- Article
- Export citation
TREE THEORY: INTERPRETABILITY BETWEEN WEAK FIRST-ORDER THEORIES OF TREES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 465-502
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELIMINATION OF IMAGINARIES IN ORDERED ABELIAN GROUPS WITH BOUNDED REGULAR RANK
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 06 February 2023, pp. 1639-1654
- Print publication:
- December 2023
-
- Article
- Export citation
INCOMPATIBILITY OF GENERIC HUGENESS PRINCIPLES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 February 2023, pp. 157-162
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTING MAXIMAL COFINITARY GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 622-651
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LARGE CARDINALS AS PRINCIPLES OF STRUCTURAL REFLECTION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 19-70
- Print publication:
- March 2023
-
- Article
- Export citation
ON THE COFINALITY OF THE LEAST
 $\lambda $-STRONGLY COMPACT CARDINAL
$\lambda $-STRONGLY COMPACT CARDINAL
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 19 January 2023, pp. 569-582
- Print publication:
- June 2024
-
- Article
- Export citation
THE PSEUDOPOWER DICHOTOMY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 1655-1681
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DIAGONAL STRONG REFLECTION PRINCIPLE AND ITS FRAGMENTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 1281-1309
- Print publication:
- September 2023
-
- Article
- Export citation
MAXIMALITY OF LOGIC WITHOUT IDENTITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 January 2023, pp. 147-162
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ITERATING THE COFINALITY-
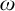 $\omega $ CONSTRUCTIBLE MODEL
$\omega $ CONSTRUCTIBLE MODEL
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 1682-1691
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
(EXTRA)ORDINARY EQUIVALENCES WITH THE ASCENDING/DESCENDING SEQUENCE PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 December 2022, pp. 262-307
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sequential and distributive forcings without choice
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 29 December 2022, pp. 868-880
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 737-752
- Print publication:
- March 2024
-
- Article
- Export citation
REFLECTION IN SECOND-ORDER SET THEORY WITH ABUNDANT URELEMENTS BI-INTERPRETS A SUPERCOMPACT CARDINAL
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 December 2022, pp. 1007-1043
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISJUNCTION AND EXISTENCE PROPERTIES IN MODAL ARITHMETIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 December 2022, pp. 178-205
- Print publication:
- March 2024
-
- Article
- Export citation
SELF-EMBEDDINGS OF MODELS OF ARITHMETIC; FIXED POINTS, SMALL SUBMODELS, AND EXTENDABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2022, pp. 1044-1066
- Print publication:
- September 2024
-
- Article
- Export citation
SUSLIN TREE PRESERVATION AND CLUB ISOMORPHISMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 December 2022, pp. 298-309
- Print publication:
- March 2025
-
- Article
- Export citation