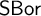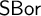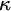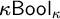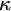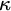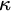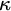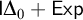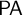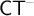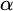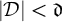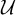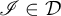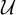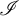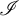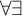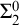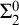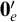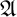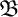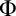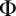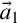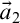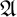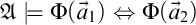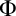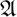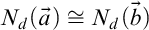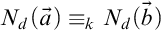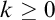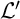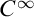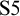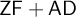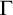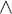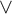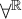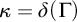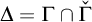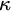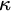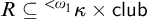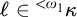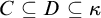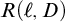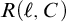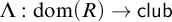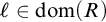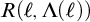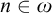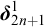Logic is traditionally considered to be a purely syntactic discipline, at least in principle. However, prof. David Isles has shown that this ideal is not yet met in traditional logic. Semantic residue is present in the assumption that the domain of a variable should be fixed in advance of a derivation, and also in the notion that a numerical notation must refer to a number rather than be considered a mathematical object in and of itself. Based on his work, the central question of this thesis is what kind of logic, if any, results from removing this semantic residue from traditional logic.
We differ from traditional logic in two significant ways. The first is that the assumption that a numerical notation must refer to a number is denied. Numerical notations are considered as mathematical objects in their own right, related to each other by means of rewrite rules. The traditional notion of reference is then replaced by the notion of reduction (by means of the rewrite rules) to a normal form. Two numerical notations that reduce to the same normal form would traditionally be considered identical, as they would refer to the same number, and hence they would be interchangeable salva veritate. In the new system, called Buridan-Volpin (BV), the numerical notations themselves are the elements of the domains of variables, and two numerical notations that reduce to the same normal form need not be interchangeable salva veritate, except when they are syntactically identical (i.e., have the same Gödel number).
The second is that we do away with the assumption that the domains of variables need to be fixed in advance of a derivation. Instead we focus on what is needed to guarantee preservation of truth in every step of a derivation. These conditions on the domains of the variables, accumulated in the course of a derivation, are combined in a reference grammar. Whereas traditionally a derivation is considered valid when the conclusion follows from the premisses by way of the derivation rules (and possibly axioms), in the BV system a derivation must meet the extra condition that no inconsistency occurs within the reference grammar. For if the reference grammar were to give rise to inconsistency (i.e., it would be impossible to assign domains to all the variables without breaking at least one of the conditions placed on them in the reference grammar), there is no longer a guarantee that truth has been preserved in every step of the derivation, and hence the truth of the conclusion is not guaranteed by the derivation.
In Chapter 2 the BV system is introduced in some formal detail. Chapter 3 gives some examples of derivations, notably totality of addition, multiplication and exponentiation, as well as a lemma needed for the proof of Euclid’s Theorem. These examples, taken from prof. Isles’ First-Order Reasoning and Primitive Recursive Natural Number Notations, show that there is a real proof-theoretical difference between traditional logic and the BV system. Here we also find the first major point of departure between myself and prof. Isles, centered on the notion of inheritance of conditions in the reference grammar by way of lemmata. These different points of view are best illustrated in the sections on the totality of exponentiation and on Euclid’s Lemma: prof. Isles maintains that the proof of totality of exponentiation is not BV valid, while I maintain that it is. But I do agree with him that the traditional proof of Euclid’s Lemma is not BV valid. Chapter 6 also expands the arguments for my choice in this matter.
Now that it has been shown that there is a difference between traditional logic and BV, the properties of BV need to be examined. In Chapter 4 we give a proof of Cut-elimination for BV minus induction and the subformula property for BV, which allows us to prove the consistency of BV minus induction. We also expand on the reasons for excluding induction. In Chapter 5 we consider in detail the proof of a finite analog to the Löwenheim–Skolem theorem given by prof. Isles in his article with the same title. He proves that under certain conditions it is always possible, given the existence of a (possibly uncountable) model for a derivation, to give a finite model for this derivation. The system he considers deviates from BV as considered in this thesis in two significant ways: it does not contain the induction rule and the domains contain numbers instead of numerical notations. We then go on to show that it is possible to extend the result to include induction, in the sense that the existence of a possibly uncountable model for a derivation guarantees the existence of a model that is at most countable. We also consider the complications that arise from taking numerical expressions instead of numbers as the elements of domains.
Finally, in Chapter 6 we consider the philosophical consequences of the BV system, informed by the formal results from the previous chapters. In particular we discuss the relation between reduction and reference, the status of reference grammars, the notion of induction and its function within BV, and some brief considerations on the consequences of the BV system for the discussion regarding nominalism and realism with regard to mathematical objects. The object of the chapter is twofold. On the one hand applying the formal results to philosophical questions, on the other hand arguing that BV is not just a theoretically acceptable alternative to traditional logic, but is in fact deserving of further development and research into its properties. The latter will probably appeal most to those of a nominalist and/or finitist bent.
Abstract prepared by Harrie de Swart and Sven Storms.
E-mail: sven.storms@tilburguniversity.edu
URL: https://research.tilburguniversity.edu/files/61701294/Storms_The_ Buridan_Volpin_04_05_2022.pdf
 $_1$-LIKE INDEPENDENCE IN AECATS
$_1$-LIKE INDEPENDENCE IN AECATS
 $\mathscr {I}$-ULTRAFILTERS IN THE RATIONAL PERFECT SET MODEL
$\mathscr {I}$-ULTRAFILTERS IN THE RATIONAL PERFECT SET MODEL