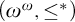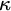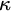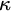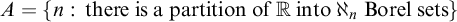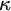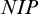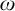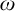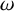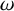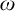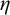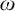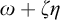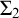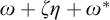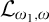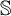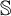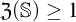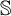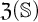Refine listing
Actions for selected content:
1095 results in 03xxx
STRUCTURE OF SUMMABLE TALL IDEALS UNDER KATĚTOV ORDER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 April 2023, pp. 725-751
- Print publication:
- June 2025
-
- Article
- Export citation
SEPARATING MANY LOCALISATION CARDINALS ON THE GENERALISED BAIRE SPACE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 April 2023, pp. 1212-1231
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARTITIONING THE REAL LINE INTO BOREL SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 549-568
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFINITARY LOGIC HAS NO EXPRESSIVE EFFICIENCY OVER FINITARY LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1817-1834
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURAL PROPERTIES OF THE STABLE CORE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 889-918
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REMARKS ON CONVERGENCE OF MORLEY SEQUENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1339-1357
- Print publication:
- September 2024
-
- Article
- Export citation
COMPARING COMPUTABILITY IN TWO TOPOLOGIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 1232-1250
- Print publication:
- September 2024
-
- Article
- Export citation
CANONICITY IN POWER AND MODAL LOGICS OF FINITE ACHRONAL WIDTH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 March 2023, pp. 705-735
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FIRST-ORDER RELEVANT REASONERS IN CLASSICAL WORLDS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2023, pp. 793-818
- Print publication:
- September 2024
-
- Article
- Export citation
THE EMBEDDING PROPERTY FOR SORTED PROFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1005-1037
- Print publication:
- September 2023
-
- Article
- Export citation
On
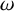 $\omega $-Strongly Measurable Cardinals
$\omega $-Strongly Measurable Cardinals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 March 2023, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ALGORITHMIC IMPOSSIBLE-WORLDS MODEL OF BELIEF AND KNOWLEDGE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 13 March 2023, pp. 586-610
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON COHESIVE POWERS OF LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 947-1004
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASSICAL MODAL THEORY OF LAWLESS SEQUENCES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 406-452
- Print publication:
- September 2023
-
- Article
- Export citation
THEORIES WITH DISTAL SHELAH EXPANSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 1323-1333
- Print publication:
- December 2023
-
- Article
- Export citation
TIGHT EVENTUALLY DIFFERENT FAMILIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 March 2023, pp. 697-723
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHICH CLASSES OF STRUCTURES ARE BOTH PSEUDO-ELEMENTARY AND DEFINABLE BY AN INFINITARY SENTENCE?
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1-18
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE ZHOU ORDINAL OF LABELLED MARKOV PROCESSES OVER SEPARABLE SPACES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 1011-1032
- Print publication:
- December 2023
-
- Article
- Export citation
AXIOMS FOR TYPE-FREE SUBJECTIVE PROBABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 493-508
- Print publication:
- June 2024
-
- Article
- Export citation
Multisummability for generalized power series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 458-494
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation