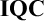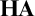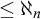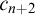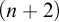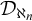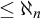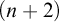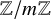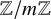Refine listing
Actions for selected content:
1095 results in 03xxx
ASYMMETRIC CUT AND CHOOSE GAMES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 July 2023, pp. 588-625
- Print publication:
- December 2023
-
- Article
- Export citation
INTERLEAVING LOGIC AND COUNTING
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 503-587
- Print publication:
- December 2023
-
- Article
- Export citation
EXTENDED FRAMES AND SEPARATIONS OF LOGICAL PRINCIPLES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 311-353
- Print publication:
- September 2023
-
- Article
- Export citation
FRACTAL DIMENSIONS OF k-AUTOMATIC SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 1128-1157
- Print publication:
- September 2024
-
- Article
- Export citation
‘A REMARKABLE ARTIFICE’: LAPLACE, POISSON AND MATHEMATICAL PURITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1018-1054
- Print publication:
- December 2024
-
- Article
- Export citation
COFINAL TYPES BELOW
 $\aleph _\omega $
$\aleph _\omega $
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1581-1606
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the class of all the rings
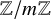 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONNEXIVE IMPLICATIONS IN SUBSTRUCTURAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 878-909
- Print publication:
- September 2024
-
- Article
- Export citation
ABELIAN GROUPS DEFINABLE IN p-ADICALLY CLOSED FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 July 2023, pp. 460-481
- Print publication:
- March 2025
-
- Article
- Export citation
TESTING DEFINITIONAL EQUIVALENCE OF THEORIES VIA AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1097-1118
- Print publication:
- December 2024
-
- Article
- Export citation
SELF-DIVISIBLE ULTRAFILTERS AND CONGRUENCES IN
 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1180-1197
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEDEKIND-FINITE CARDINALS HAVING COUNTABLE PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1308-1323
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBJECT-MATTER AND INTENSIONAL OPERATORS III: STATE-SENSITIVE SUBJECT-MATTER AND TOPIC SUFFICIENCY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1070-1096
- Print publication:
- December 2024
-
- Article
- Export citation
A SIMPLIFIED PROOF OF THE EPSILON THEOREMS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1248-1263
- Print publication:
- December 2024
-
- Article
- Export citation
A NATURAL DEDUCTION SYSTEM FOR ORTHOMODULAR LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 910-949
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSICAL DETERMINATE TRUTH I
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 218-261
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELEMENTARY EQUIVALENCE IN POSITIVE LOGIC VIA PRIME PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 05 July 2023, pp. 1129-1146
- Print publication:
- September 2025
-
- Article
- Export citation
COMPUTABLE VS DESCRIPTIVE COMBINATORICS OF LOCAL PROBLEMS ON TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1835-1849
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparse analytic systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RELEVANT CONSEQUENCE RELATIONS: AN INVITATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 762-792
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation