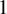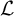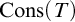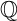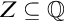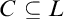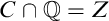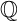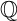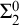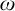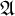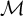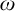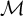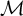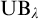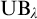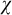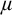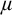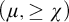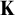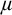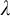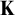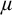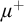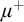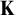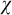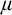Refine listing
Actions for selected content:
1095 results in 03xxx
UNDEFINABILITY OF MULTIPLICATION IN PRESBURGER ARITHMETIC WITH SETS OF POWERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 10 October 2023, pp. 872-886
- Print publication:
- June 2025
-
- Article
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE UNDECIDABILITY IN NIP FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 04 October 2023, pp. 509-532
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEAK INDESTRUCTIBILITY AND REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 980-1006
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TOPOLOGICAL APPROACH TO UNDEFINABILITY IN ALGEBRAIC EXTENSIONS OF
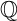 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 September 2023, pp. 626-655
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DECIDABLE FRAGMENTS OF THE QUANTIFIED ARGUMENT CALCULUS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 September 2023, pp. 736-761
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALGEBRAIC SEMANTICS FOR RELATIVE TRUTH, AWARENESS, AND POSSIBILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 154-177
- Print publication:
- March 2024
-
- Article
- Export citation
WEAK WELL ORDERS AND FRAÏSSÉ’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A PROOF COMPLEXITY CONJECTURE AND THE INCOMPLETENESS THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 19 September 2023, pp. 1206-1210
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSIFICATION OF
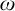 $\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
$\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 460-495
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLE TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 September 2023, pp. 188-220
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COLORING ISOSCELES TRIANGLES IN CHOICELESS SET THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 105-134
- Print publication:
- March 2025
-
- Article
- Export citation
ON COHEN AND PRIKRY FORCING NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 858-904
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THORN FORKING, WEAK NORMALITY, AND THEORIES WITH SELECTORS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1354-1366
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
USUBA’S PRINCIPLE
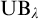 $\mathrm {UB}_\lambda $ CAN FAIL AT SINGULAR CARDINALS
$\mathrm {UB}_\lambda $ CAN FAIL AT SINGULAR CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 195-203
- Print publication:
- March 2024
-
- Article
- Export citation
WEAK HEIRS, COHEIRS, AND THE ELLIS SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 166-187
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON HALFWAY NEW CARDINAL CHARACTERISTICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1324-1339
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROOF SYSTEMS FOR TWO-WAY MODAL μ-CALCULUS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1211-1260
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STABILITY RESULTS ASSUMING TAMENESS, MONSTER MODEL, AND CONTINUITY OF NONSPLITTING
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 383-425
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ORTHOGONAL DECOMPOSITION OF DEFINABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 August 2023, pp. 1158-1179
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation