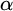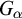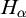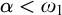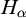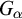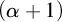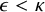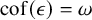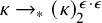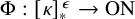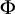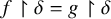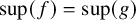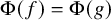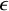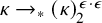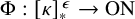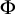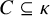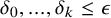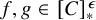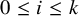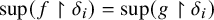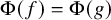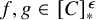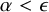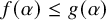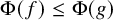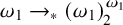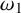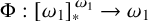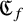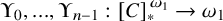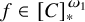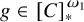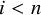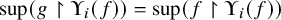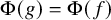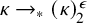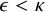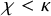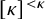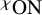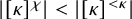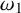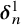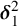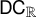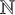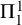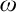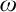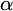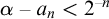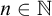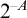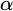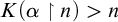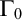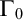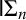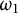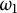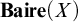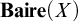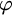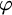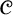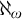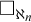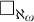Refine listing
Actions for selected content:
1095 results in 03xxx
VERY LARGE SET AXIOMS OVER CONSTRUCTIVE SET THEORIES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 455-535
- Print publication:
- December 2024
-
- Article
- Export citation
CONCEPTUAL DISTANCE AND ALGEBRAS OF CONCEPTS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 February 2024, pp. 300-315
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
ON RANK NOT ONLY IN NSOP
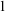 $_1$ THEORIES
$_1$ THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1669-1702
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
THE PENTAGON AS A SUBSTRUCTURE LATTICE OF MODELS OF PEANO ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1078-1097
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost Everywhere Behavior of Functions According to Partition Measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functorial Fast-Growing Hierarchies
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 January 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CATEGORICAL QUANTIFICATION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 24 January 2024, pp. 227-252
- Print publication:
- June 2024
-
- Article
- Export citation
REGAININGLY APPROXIMABLE NUMBERS AND SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINCARÉ–WEYL’S PREDICATIVITY: GOING BEYOND
 $\Gamma _{0}$
$\Gamma _{0}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 41-91
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1798-1816
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WALK WITH GOODSTEIN
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-19
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel reducibility of equivalence relations on
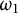 $\omega _1$
$\omega _1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 687-700
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On definable groups and D-groups in certain fields with a generic derivation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 15 January 2024, pp. 459-480
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-TRIVIAL HIGHER HOMOTOPY OF FIRST-ORDER THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 January 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGREE OF SATISFIABILITY IN HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2024, pp. 533-551
- Print publication:
- June 2025
-
- Article
- Export citation
THE BAIRE CLOSURE AND ITS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 27-49
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORBIDDEN INDUCED SUBGRAPHS AND THE ŁOŚ–TARSKI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 516-548
- Print publication:
- June 2024
-
- Article
- Export citation
ON COMPACTNESS OF WEAK SQUARE AT SINGULARS OF UNCOUNTABLE COFINALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 January 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
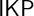
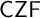
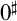
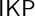
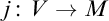
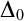
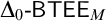
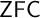
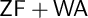


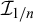
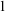










 -stationary. We give natural examples of families of invariant types satisfying this property in some NSOP
-stationary. We give natural examples of families of invariant types satisfying this property in some NSOP