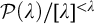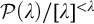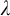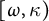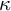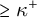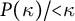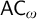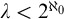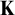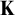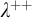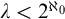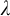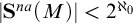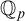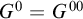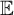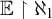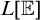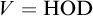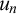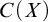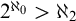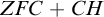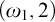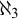Refine listing
Actions for selected content:
1095 results in 03xxx
STRONG COMPLETENESS OF A FIRST-ORDER TEMPORAL LOGIC FOR REAL TIME
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 22 May 2024, pp. 527-544
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\Delta ^1_1$ EFFECTIVIZATION IN BOREL COMBINATORICS
$\Delta ^1_1$ EFFECTIVIZATION IN BOREL COMBINATORICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 943-967
- Print publication:
- September 2025
-
- Article
- Export citation
ON AUTOMORPHISMS OF
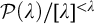 ${\mathcal {P}}(\lambda )/[\lambda ]^{<\lambda }$
${\mathcal {P}}(\lambda )/[\lambda ]^{<\lambda }$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1476-1512
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stereographic compactification and affine bi-Lipschitz homeomorphisms
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 582-596
- Print publication:
- September 2024
-
- Article
- Export citation
META-CLASSICAL NON-CLASSICAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1146-1171
- Print publication:
- December 2024
-
- Article
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 830-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STRUCTURE OF BOCHVAR ALGEBRAS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 273-299
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POUR-EL’S LANDSCAPE
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 09 May 2024, pp. 362-397
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributivity and base trees for
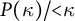 $P(\kappa)/ {\lt} \kappa$
$P(\kappa)/ {\lt} \kappa$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 915-926
- Print publication:
- December 2024
-
- Article
- Export citation
DOES
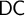 $\mathsf {DC}$ IMPLY
$\mathsf {DC}$ IMPLY 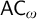 ${\mathsf {AC}}_\omega $, UNIFORMLY?
${\mathsf {AC}}_\omega $, UNIFORMLY?
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BUILDING MODELS IN SMALL CARDINALS IN LOCAL ABSTRACT ELEMENTARY CLASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ONE-DIMENSIONAL SUBGROUPS AND CONNECTED COMPONENTS IN NON-ABELIAN p-ADIC DEFINABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-19
-
- Article
- Export citation
GENERIC EXPANSIONS OF GEOMETRIC THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1056-1077
- Print publication:
- September 2025
-
- Article
- Export citation
COUNTING IN UNCOUNTABLY CATEGORICAL PSEUDOFINITE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1455-1475
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DEFINABILITY OF THE EXTENDER SEQUENCE
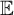 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM 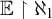 $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN 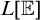 $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCONTINUOUS HOMOMORPHISMS OF
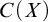 $C(X)$ WITH
$C(X)$ WITH 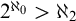 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 665-696
- Print publication:
- June 2024
-
- Article
- Export citation
THE TEMPORAL CONTINUUM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 April 2024, pp. 420-438
- Print publication:
- June 2025
-
- Article
- Export citation
THE AMALGAMATION PROPERTY AND URYSOHN STRUCTURES IN CONTINUOUS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON GALOIS COHOMOLOGY, DEFINABILITY, AND DIFFERENTIAL ALGEBRAIC GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 496-515
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation