Refine listing
Actions for selected content:
1095 results in 03xxx
ON INDESTRUCTIBLE STRONGLY GUESSING MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-27
-
- Article
- Export citation
THE ERDŐS–HAJNAL PROBLEM LIST
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 418-461
- Print publication:
- September 2025
-
- Article
- Export citation
CATEGORICAL FOUNDATIONS OF FORMALIZED CONDENSED MATHEMATICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 31 December 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLIANCE AND COMMAND III: CONDITIONAL IMPERATIVES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 52-98
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GENERIC MULTIVERSE IS NOT GOING AWAY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 671-703
- Print publication:
- September 2025
-
- Article
- Export citation
UNIVOCITY OF INTUITIONISTIC AND CLASSICAL CONNECTIVES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 488-497
- Print publication:
- September 2025
-
- Article
- Export citation
WHAT STANDS BETWEEN GROUNDING RULES AND LOGICAL RULES IS THE EXCLUDED MIDDLE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-27
- Print publication:
- March 2025
-
- Article
- Export citation
Structural convergence and algebraic roots
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 392-400
-
- Article
- Export citation
LOCAL FINITENESS IN VARIETIES OF MS4-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ordinary differentially large fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABLE HENSELIAN VALUATIONS IN POSITIVE RESIDUE CHARACTERISTIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COMPACTNESS OF GÖDEL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-10
-
- Article
- Export citation
ON THE EXPRESSIVE POWER OF INQUISITIVE EPISTEMIC LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SATISFACTION CLASSES WITH APPROXIMATE DISJUNCTIVE CORRECTNESS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 545-562
- Print publication:
- June 2025
-
- Article
- Export citation
Quasiminimality of complex powers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e123
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCRETE SETS DEFINABLE IN STRONG EXPANSIONS OF ORDERED ABELIAN GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 423-459
- Print publication:
- March 2025
-
- Article
- Export citation
SCOTT SENTENCE COMPLEXITIES OF LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-30
-
- Article
- Export citation
CERTIFIED
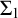 $ \Sigma _1$-SENTENCES
$ \Sigma _1$-SENTENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE-DIMENSIONAL DIFFERENTIAL-ALGEBRAIC PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 603-626
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\gamma $-ADMISSIBILITY IN FIRST-ORDER RELEVANT LOGICS: PROOF USING NORMAL MODELS IN THE MARES–GOLDBLATT SETTING
$\gamma $-ADMISSIBILITY IN FIRST-ORDER RELEVANT LOGICS: PROOF USING NORMAL MODELS IN THE MARES–GOLDBLATT SETTING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 398-419
- Print publication:
- June 2025
-
- Article
- Export citation
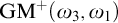
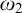
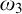
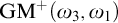
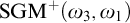
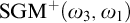
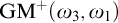
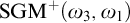
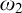















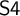
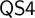
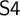
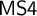
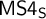
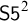
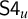
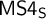
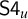
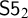
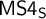
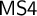
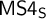
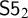














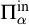
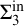
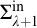
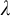
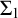
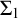
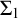
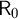
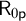
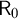
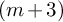
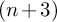



 of a wide range of propositional relevant logics for which excluded middle is valid (with fusion and the Ackermann truth constant), the first-order extensions
of a wide range of propositional relevant logics for which excluded middle is valid (with fusion and the Ackermann truth constant), the first-order extensions  and
and  admit
admit 


