Refine listing
Actions for selected content:
1092 results in 03xxx
POLYMORPHISM AND MINIMAL TYPES WITHOUT DEPENDENT PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 March 2025, pp. 1-33
-
- Article
- Export citation
MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 194-200
- Print publication:
- August 2025
-
- Article
- Export citation
NEW FOUNDATIONS OF REASONING VIA REAL-VALUED FIRST-ORDER LOGICS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 319-349
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BI-CONNEXIVE LOGIC, BILATERALISM, AND NEGATION INCONSISTENCY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 859-899
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GLOBAL SUPERVENIENCE IN INQUISITIVE MODAL LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 589-615
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SEPARATING WHOLENESS AXIOMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1-24
-
- Article
- Export citation
FROM REAL ANALYSIS TO THE SORITES PARADOX VIA REVERSE MATHEMATICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 900-926
- Print publication:
- September 2025
-
- Article
- Export citation
On the algorithmic descriptive complexity of attractors in topological dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2533-2560
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IS THERE A COUNTABLE OMEGA-UNIVERSAL LOGIC?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 963-970
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MENGER AND CONSONANT SETS IN THE SACKS MODEL
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 March 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIVERSALITY PROPERTIES OF FORCING
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 March 2025, pp. 1-19
-
- Article
- Export citation
HEREDITARILY STRUCTURALLY COMPLETE EXTENSIONS OF
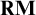 ${\mathbf {RM}}$
${\mathbf {RM}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 March 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE TRANSCENDENCE DEGREE OF THE REALS OVER CERTAIN SET-THEORETICAL SUBFIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-18
-
- Article
- Export citation
THE KAUFMANN–CLOTE QUESTION ON END EXTENSIONS OF MODELS OF ARITHMETIC AND THE WEAK REGULARITY PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FORMALISATION OF CONSTRUCTIVE EVIDENCE-BASED REASONING: CONSTRUCTING JUSTIFICATIONS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-25
-
- Article
- Export citation
A MODULAR BISIMULATION CHARACTERISATION FOR FRAGMENTS OF HYBRID LOGIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-29
-
- Article
- Export citation
ON A CONJECTURE REGARDING THE MOUSE ORDER FOR WEASELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 364-390
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE NON-EXISTENCE OF PRIME MODELS OF THEORIES OF PSEUDO-FINITE FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 52-67
- Print publication:
- March 2025
-
- Article
- Export citation
A DEFENSE OF LOGICISM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 88-152
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SOME OF BROUWER’S AXIOMS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-52
- Print publication:
- March 2025
-
- Article
- Export citation























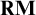
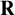
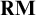
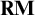
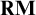
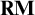
























 -Woodin cardinal. On the other hand, we show thatassuming there is no transitive model of KP with a Woodin cardinal theconjecture holds. In the course of this we will also show that if
-Woodin cardinal. On the other hand, we show thatassuming there is no transitive model of KP with a Woodin cardinal theconjecture holds. In the course of this we will also show that if







