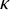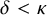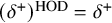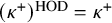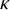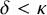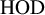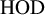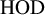Refine listing
Actions for selected content:
1092 results in 03xxx
A classification of incompleteness statements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 24 July 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TWO-SORTED THEORY OF NILPOTENT LIE ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compactness phenomena in HOD
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RAMSEY-LIKE THEOREMS FOR THE SCHREIER BARRIER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 July 2025, pp. 1-29
-
- Article
- Export citation
TOPICS, NON-UNIFORM SUBSTITUTIONS, AND VARIABLE SHARING
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RNMATRICES FOR MODAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 July 2025, pp. 744-774
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTUM EXPANDERS AND QUANTIFIER REDUCTION FOR TRACIAL VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ÉTALE STRUCTURES AND THE JOYAL–TIERNEY REPRESENTATION THEOREM IN COUNTABLE MODEL THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 July 2025, pp. 1-52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elementary equivalence and disintegration of tracial von Neumann algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 July 2025, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FAILURE OF BETH’S THEOREM IN RELEVANCE LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 949-962
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WALK ON THE WILD SIDE: NOTIONS OF MAXIMALITY IN FIRST-ORDER THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 June 2025, pp. 1-31
-
- Article
- Export citation
A model of the Axiom of Determinacy in which every set of reals is universally Baire
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 June 2025, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PRODUCTS OF ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-17
-
- Article
- Export citation
PROOF MINING AND THE CONVEX FEASIBILITY PROBLEM: THE CURIOUS CASE OF DYKSTRA’S ALGORITHM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 775-811
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CONSTRUCTIVE INTERPRETATION OF THE LOGICAL CONSTANTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 October 2025, pp. 288-318
- Print publication:
- June 2025
-
- Article
- Export citation
CORONA RIGIDITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 195-287
- Print publication:
- June 2025
-
- Article
- Export citation
Logic, Arithmetic, and Definitions
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 October 2025, p. 353
- Print publication:
- June 2025
-
- Article
-
- You have access
- Export citation
Studies on Partial Impredicativity in Formal Systems of Arithmetic and Computability Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 October 2025, pp. 352-353
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Density of monochromatic infinite subgraphs II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Echeloned Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation