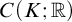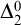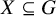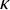Refine listing
Actions for selected content:
1092 results in 03xxx
DUALITY FOR CLANS: AN EXTENSION OF GABRIEL–ULMER DUALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 May 2025, pp. 1-38
-
- Article
- Export citation
CONTRACTING ENDOMORPHISMS OF VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 2047-2106
- Print publication:
- September 2025
-
- Article
- Export citation
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
A counterexample regarding an equivalence relation on a product space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-5
-
- Article
- Export citation
DP AND OTHER MINIMALITIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-30
-
- Article
- Export citation
The nonabelian product modulo sum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1069-1109
-
- Article
- Export citation
COMPUTABLE TYPE OF CERTAIN QUOTIENT SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-31
-
- Article
- Export citation
PFA AND THE DEFINABILITY OF THE NONSTATIONARY IDEAL
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-8
-
- Article
- Export citation
ON THE PROOF-THEORETIC STRUCTURE OF COUNTERFACTUAL INFERENCE
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF DIFFERENTIAL-HENSELIAN PRE-H-FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGH DIMENSIONAL COUNTABLE COMPACTNESS AND ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-21
-
- Article
- Export citation
COLORING EQUILATERAL TRIANGLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-14
-
- Article
- Export citation
ENRICHED CONCEPTS OF REGULAR LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 2695-2723
- Print publication:
- September 2025
-
- Article
- Export citation
MINIMAL MODAL LOGICS, CONSTRUCTIVE MODAL LOGICS AND THEIR RELATIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 27 March 2025, pp. 463-504
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTEREXAMPLES IN EFFECTIVE TOPOLOGY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Shelah group in ZFC
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ORDER ANALYSIS OF HYPERFINITE BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-23
-
- Article
- Export citation
Linearity of compact R-analytic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 787-794
-
- Article
-
- You have access
- Open access
- HTML
- Export citation