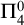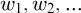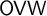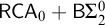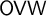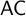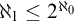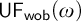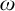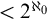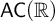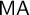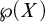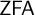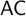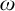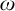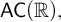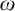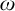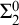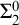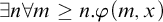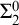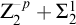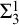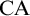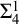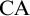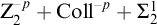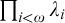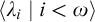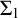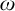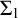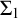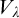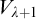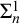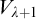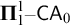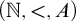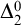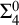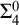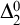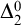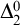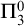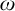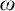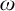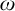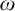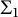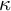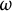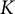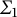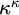Refine listing
Actions for selected content:
1095 results in 03xxx
A RIGID KUREPA TREE FROM A FREE SUSLIN TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 1198-1205
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COVERING NUMBERS OF SOME MYCIELSKI IDEALS MAY BE DIFFERENT
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 252-277
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
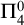 $\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
$\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
ON PROVING CONSISTENCY OF EQUATIONAL THEORIES IN BOUNDED ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 135-165
- Print publication:
- March 2025
-
- Article
- Export citation
ON FREE ULTRAFILTERS ON
 $\omega $ WITH WELL-ORDERABLE BASES IN
$\omega $ WITH WELL-ORDERABLE BASES IN  $\mathsf {ZF}$
$\mathsf {ZF}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MANY-ONE REDUCIBILITY WITH REALIZABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-39
-
- Article
- Export citation
PARAMETER-FREE SCHEMES IN SECOND-ORDER ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-19
-
- Article
- Export citation
Rich representations and superrigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2249-2272
- Print publication:
- August 2025
-
- Article
- Export citation
DESCRIPTIVE PROPERTIES OF I2-EMBEDDINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUFFICIENT CONDITIONS FOR LOCAL TABULARITY OF A POLYMODAL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 655-680
- Print publication:
- June 2025
-
- Article
- Export citation
THE WEIHRAUCH LATTICE AT THE LEVEL OF
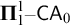 $\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM
$\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 752-790
- Print publication:
- June 2025
-
- Article
- Export citation
THE COMPLEXITY OF ORDER-COMPUTABLE SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-24
-
- Article
- Export citation
A SIMPLIFIED LOWER BOUND FOR IMPLICATIONAL LOGIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 53-87
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OMEGA-CATEGORICAL PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On
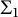 $\Sigma _1$-definable closed unbounded sets
$\Sigma _1$-definable closed unbounded sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LATTICE PROBLEM FOR MODELS OF
 $\mathsf {PA}$
$\mathsf {PA}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-28
-
- Article
- Export citation
THE ALGEBRAS OF LEWIS’S COUNTERFACTUALS: AXIOMATIZATIONS AND ALGEBRAIZABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 563-588
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALIZED TOWER SPECTRA
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 January 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FEFERMAN’S COMPLETENESS THEOREM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 462-487
- Print publication:
- September 2025
-
- Article
- Export citation