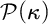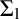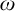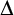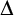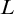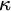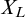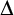Refine listing
Actions for selected content:
1095 results in 03xxx
A RECURSIVE COLORING FUNCTION WITHOUT
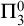 $ \Pi _3^0$ SOLUTIONS FOR HINDMAN’S THEOREM
$ \Pi _3^0$ SOLUTIONS FOR HINDMAN’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-24
-
- Article
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1329-1369
- Print publication:
- May 2025
-
- Article
- Export citation
REFERENCE DIGRAPHS OF NON-SELF-REFERENTIAL PARADOXES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 349-366
- Print publication:
- March 2025
-
- Article
- Export citation
A PARAMETERIZED HALTING PROBLEM,
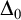 $ \Delta _0$ TRUTH AND THE MRDP THEOREM
$ \Delta _0$ TRUTH AND THE MRDP THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 483-508
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GROUPS AND FIELDS DEFINABLE IN
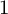 $1$-H-MINIMAL FIELDS
$1$-H-MINIMAL FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 203-248
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The definable content of homological invariants II: Čech cohomology and homotopy classification
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARTIN–SCHREIER EXTENSIONS AND COMBINATORIAL COMPLEXITY IN HENSELIAN VALUED FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1747-1767
- Print publication:
- December 2024
-
- Article
- Export citation
NORMALISATION FOR NEGATIVE FREE LOGICS WITHOUT AND WITH DEFINITE DESCRIPTIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 September 2024, pp. 240-272
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON CONTINUOUS FUNCTIONS ON METRIC SPACES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 January 2025, pp. 398-420
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANSELM’S ONTOLOGICAL ARGUMENT AND GRADES OF BEING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 635-653
- Print publication:
- September 2024
-
- Article
- Export citation
A CLUB GUESSING TOOLBOX I
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 January 2025, pp. 303-361
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Note on almost isometric ideals and local retracts in Banach and metric spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-25
-
- Article
- Export citation
LIMIT COMPLEXITIES, MINIMAL DESCRIPTIONS, AND n-RANDOMNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 05 June 2024, pp. 1261-1276
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proof-Theoretical Aspects of Nonlinear and Set-Valued Analysis
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 November 2024, pp. 288-289
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
From real-life to very strong axioms. Classification problems in Descriptive Set Theory and regularity properties in Generalized Descriptive Set Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 November 2024, pp. 285-286
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Many problems, different frameworks: classification of problems in computable analysis and algorithmic learning theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 November 2024, pp. 287-288
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
FINITARY UPPER LOGICISM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1172-1247
- Print publication:
- December 2024
-
- Article
- Export citation
The Galvin property under the ultrapower axiom
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 27 May 2024, pp. 1686-1717
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVARIANT KEISLER MEASURES FOR
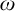 $\omega $-CATEGORICAL STRUCTURES
$\omega $-CATEGORICAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 22 May 2024, pp. 791-807
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIAMOND ON LADDER SYSTEMS AND COUNTABLY METACOMPACT TOPOLOGICAL SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
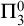
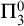
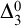
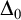






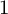
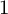
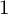
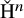 on the category of locally compact separable metric spaces each factor into (i) what we term their
on the category of locally compact separable metric spaces each factor into (i) what we term their 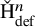 taking values in the category
taking values in the category 

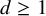
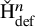 to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement
to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement 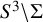
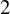
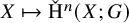 admit two main formulations: a more combinatorial one and a more homotopical formulation as the group
admit two main formulations: a more combinatorial one and a more homotopical formulation as the group 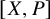
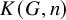
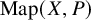
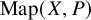
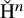 , embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if
, embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if 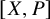




 operator for definite descriptions. Rules specific to free logic give rise to new kinds of maximal formulas additional to those familiar from standard intuitionist and classical logic. When
operator for definite descriptions. Rules specific to free logic give rise to new kinds of maximal formulas additional to those familiar from standard intuitionist and classical logic. When  is added it must be ensured that reduction procedures involving replacements of parameters by terms do not introduce new maximal formulas of higher degree than the ones removed. The problem is solved by a rule that permits restricting these terms in the rules for
is added it must be ensured that reduction procedures involving replacements of parameters by terms do not introduce new maximal formulas of higher degree than the ones removed. The problem is solved by a rule that permits restricting these terms in the rules for 

 to parameters or constants. A restricted subformula property for deductions in systems without
to parameters or constants. A restricted subformula property for deductions in systems without  is considered. It is improved upon by an alternative formalisation of free logic building on an idea of Jaśkowski’s. In the classical system the rules for
is considered. It is improved upon by an alternative formalisation of free logic building on an idea of Jaśkowski’s. In the classical system the rules for  require treatment known from normalisation for classical logic with
require treatment known from normalisation for classical logic with