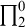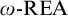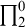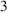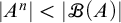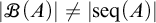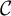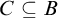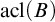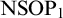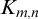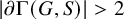Refine listing
Actions for selected content:
1095 results in 03xxx
A
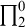 $ \prod _{2}^{0}$ SINGLETON OF MINIMAL ARITHMETIC DEGREE
$ \prod _{2}^{0}$ SINGLETON OF MINIMAL ARITHMETIC DEGREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic Stability Independence and Treeless Theories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ITERATED PRIORITY ARGUMENTS IN DESCRIPTIVE SET THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 199-226
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CANTOR’S THEOREM MAY FAIL FOR FINITARY PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-18
-
- Article
- Export citation
NONDEFINABILITY RESULTS FOR ELLIPTIC AND MODULAR FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ONE-VARIABLE FRAGMENTS OF FIRST-ORDER LOGICS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 253-278
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WAND/SET THEORIES: A REALIZATION OF CONWAY’S MATHEMATICIANS’ LIBERATION MOVEMENT, WITH AN APPLICATION TO CHURCH’S SET THEORY WITH A UNIVERSAL SET
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON QUANTIFICATION AND EXTENSIONALITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 343-365
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE FRAGILITY OF INTERPOLATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS AND LIMITS OF THE SPECKER–BLATTER THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1284-1312
- Print publication:
- September 2024
-
- Article
- Export citation
THREE SURPRISING INSTANCES OF DIVIDING
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A LOPEZ-ESCOBAR THEOREM FOR CONTINUOUS DOMAINS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 15 March 2024, pp. 854-871
- Print publication:
- June 2025
-
- Article
- Export citation
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO-CARDINAL DERIVED TOPOLOGIES, INDESCRIBABILITY AND RAMSEYNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperfiniteness of boundary actions of acylindrically hyperbolic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW PERSPECTIVE ON SEMI-RETRACTIONS AND THE RAMSEY PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 945-979
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DUALITY FOR COALGEBRAS FOR VIETORIS AND MONADICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1022-1055
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARROW’S THEOREM, ULTRAFILTERS, AND REVERSE MATHEMATICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 29 February 2024, pp. 439-462
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COFINAL TYPES OF ULTRAFILTERS OVER MEASURABLE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation