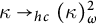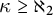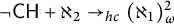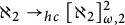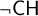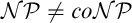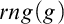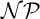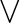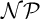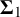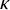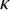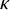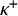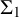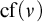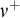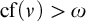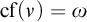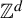Refine listing
Actions for selected content:
1095 results in 03xxx
LOGICS FROM ULTRAFILTERS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 28 November 2023, pp. 142-159
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
More Ramsey theory for highly connected monochromatic subgraphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 24 November 2023, pp. 2136-2150
- Print publication:
- December 2024
-
- Article
- Export citation
Selection principles and proofs from the Book
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 November 2023, pp. 478-492
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO EXAMPLES CONCERNING EXISTENTIAL UNDECIDABILITY IN FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 November 2023, pp. 552-563
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE EXISTENCE OF STRONG PROOF COMPLEXITY GENERATORS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 20-40
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
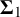 $\mathbf {\Sigma }_1$-definability at higher cardinals: Thin sets, almost disjoint families and long well-orders
$\mathbf {\Sigma }_1$-definability at higher cardinals: Thin sets, almost disjoint families and long well-orders
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BETWEENNESS ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 November 2023, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ONTOLOGICAL PURITY FOR FORMAL PROOFS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 395-434
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON UNSUPERSTABLE THEORIES IN GDST
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1720-1746
- Print publication:
- December 2024
-
- Article
- Export citation
NON-FACTIVE KOLMOGOROV CONDITIONALIZATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 October 2023, pp. 186-212
- Print publication:
- March 2025
-
- Article
- Export citation
STATIONARY REFLECTION AND THE FAILURE OF THE SCH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-26
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON SACKS’ SPLITTING THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 26 October 2023, pp. 1768-1797
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAXIMAL STABLE QUOTIENTS OF INVARIANT TYPES IN NIP THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 25 October 2023, pp. 918-942
- Print publication:
- June 2025
-
- Article
- Export citation
ON EASTON SUPPORT ITERATION OF PRIKRY-TYPE FORCING NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 25 October 2023, pp. 968-1013
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Katok’s special representation theorem for multidimensional Borel flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1945-1962
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PAC STRUCTURES AS INVARIANTS OF FINITE GROUP ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1340-1375
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ALGEBRAIC PROOF OF COMPLETENESS FOR MONADIC FUZZY PREDICATE LOGIC
 $\mathbf {MMTL}\boldsymbol {\forall }$
$\mathbf {MMTL}\boldsymbol {\forall }$
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 October 2023, pp. 213-239
- Print publication:
- March 2025
-
- Article
- Export citation
BIG IN REVERSE MATHEMATICS: MEASURE AND CATEGORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1-46
-
- Article
- Export citation
COMBINATORIAL BOUNDS IN DISTAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 October 2023, pp. 1-33
-
- Article
- Export citation