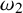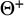Refine listing
Actions for selected content:
1092 results in 03xxx
DEFINABLE SKOLEM FUNCTIONS IN WEAKLY O-MINIMAL NON-VALUATIONAL EXPANSIONS OF ORDERED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-11
-
- Article
- Export citation
SET-THEORETIC BICONTEXTUALISM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 22 August 2025, pp. 826-858
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOGICS OF LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABSTRACTION PRINCIPLES AND THE SIZE OF REALITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 19 August 2025, pp. 812-825
- Print publication:
- September 2025
-
- Article
- Export citation
MIXED IDENTITIES FOR OLIGOMORPHIC AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TEAM SEMANTICS AND INDEPENDENCE NOTIONS IN QUANTUM PHYSICS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LYNDON INTERPOLATION PROPERTY FOR EXTENSIONS OF
 $\mathbf {S4}$ AND INTERMEDIATE PROPOSITIONAL LOGICS
$\mathbf {S4}$ AND INTERMEDIATE PROPOSITIONAL LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-33
-
- Article
- Export citation
REVERSE MATHEMATICS OF A UNIFORM KRUSKAL–FRIEDMAN THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE FINITE BASIS PROBLEM FOR FREE TREE MONOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-8
-
- Article
- Export citation
MODULAR SEQUENT CALCULI FOR INTERPRETABILITY LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 08 August 2025, pp. 704-743
- Print publication:
- September 2025
-
- Article
- Export citation
BETWEEN PROOF CONSTRUCTION AND SAT-SOLVING
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRUTH AND COLLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MEASURABLE DOMATIC PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-25
-
- Article
- Export citation
UNIFORMITY NUMBERS OF THE NULL-ADDITIVE AND MEAGER-ADDITIVE IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-37
-
- Article
- Export citation
MODELS FOR OFFICIAL ENTAILMENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 06 August 2025, pp. 927-948
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semisimple groups interpretable in various valued fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 August 2025, e127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LATTICE EMBEDDINGS AND PUNCTUAL LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEPARATING SUBVERSION FORCING AXIOMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 30 July 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\textsf {AD}^{+}$ implies
$\textsf {AD}^{+}$ implies  $ \omega _{1}$ is a club
$ \omega _{1}$ is a club  $ \Theta $-Berkeley cardinal
$ \Theta $-Berkeley cardinal
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 July 2025, e126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CARNAP’S (CATEGORICITY) PROBLEM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 July 2025, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation





































































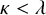
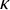

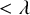


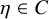


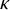
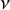
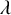




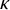

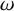



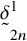 ’s are
’s are