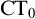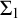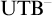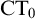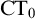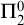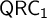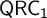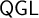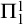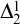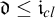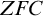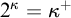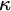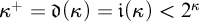Refine listing
Actions for selected content:
1095 results in 03xxx
Invariant Ideal Axiom
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY AND PROOF THEORY OF THE GLOBAL REFLECTION PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 738-779
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CELLULAR CATEGORIES AND STABLE INDEPENDENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 May 2022, pp. 811-834
- Print publication:
- June 2023
-
- Article
- Export citation
IS CAUSAL REASONING HARDER THAN PROBABILISTIC REASONING?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 18 May 2022, pp. 106-131
- Print publication:
- March 2024
-
- Article
- Export citation
Hensel minimality I
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 May 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Club stationary reflection and the special Aronszajn tree property
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 854-911
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polish spaces of Banach spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 May 2022, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ESCAPE FROM VARDANYAN’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 1613-1638
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROOF SYSTEMS FOR EXACT ENTAILMENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1260-1295
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIVERSAL CODING AND PREDICTION ON ERGODIC RANDOM POINTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 May 2022, pp. 387-412
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASPERÓ–MOTA ITERATION AND THE SIZE OF THE CONTINUUM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1387-1420
- Print publication:
- December 2023
-
- Article
- Export citation
TREE FORCING AND DEFINABLE MAXIMAL INDEPENDENT SETS IN HYPERGRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 April 2022, pp. 1419-1458
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABILITY OF HENSELIAN VALUATIONS BY CONDITIONS ON THE VALUE GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1064-1082
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURAL HIGHNESS NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1692-1724
- Print publication:
- December 2023
-
- Article
- Export citation
THE LOGIC OF HYPERLOGIC. PART A: FOUNDATIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 27 April 2022, pp. 244-271
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ORDER TYPES OF MODELS OF FRAGMENTS OF PEANO ARITHMETIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 27 April 2022, pp. 182-206
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHAT IS A RESTRICTIVE THEORY?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 25 April 2022, pp. 67-105
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGHER INDEPENDENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 1606-1630
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNDECIDABILITY AND NON-AXIOMATIZABILITY OF MODAL MANY-VALUED LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 20 April 2022, pp. 1576-1605
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO-SORTED FREGE ARITHMETIC IS NOT CONSERVATIVE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1199-1232
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation