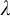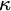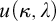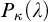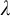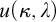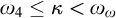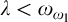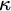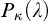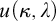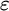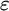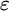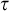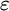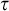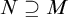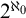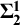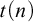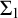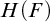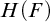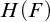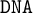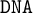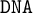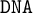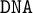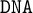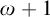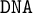Refine listing
Actions for selected content:
1095 results in 03xxx
APPLICATIONS OF PCF THEORY TO THE STUDY OF IDEALS ON
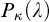
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 January 2022, pp. 967-994
- Print publication:
- September 2022
-
- Article
- Export citation
EPSILON THEOREMS IN INTERMEDIATE LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 682-720
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING SIBLINGS IN UNIVERSAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1130-1155
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLEXITY OF INDEX SETS OF DESCRIPTIVE SET-THEORETIC NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 894-911
- Print publication:
- September 2022
-
- Article
- Export citation
MODEL COMPLETIONS FOR UNIVERSAL CLASSES OF ALGEBRAS: NECESSARY AND SUFFICIENT CONDITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 381-417
- Print publication:
- March 2023
-
- Article
- Export citation
RAMSIFICATION AND SEMANTIC INDETERMINACY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 January 2022, pp. 900-950
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DISCONTINUITY PROBLEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 January 2022, pp. 1191-1212
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODES OF CONVERGENCE TO THE TRUTH: STEPS TOWARD A BETTER EPISTEMOLOGY OF INDUCTION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 January 2022, pp. 277-310
- Print publication:
- June 2022
-
- Article
- Export citation
A MINIMAL SET LOW FOR SPEED
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 03 January 2022, pp. 1693-1728
- Print publication:
- December 2022
-
- Article
- Export citation
THE GENEALOGY OF ‘
 $\mathbin {\boldsymbol {\vee }}$’
$\mathbin {\boldsymbol {\vee }}$’
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 January 2022, pp. 862-899
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERPRETING A FIELD IN ITS HEISENBERG GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1215-1230
- Print publication:
- September 2022
-
- Article
- Export citation
Stit-LOGIC FOR IMAGINATION EPISODES WITH VOLUNTARY INPUT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 813-861
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation
MONADIC INTUITIONISTIC AND MODAL LOGICS ADMITTING PROVABILITY INTERPRETATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 427-467
- Print publication:
- March 2023
-
- Article
- Export citation
AN ALGEBRAIC APPROACH TO INQUISITIVE AND
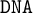 $\mathtt {DNA}$-LOGICS
$\mathtt {DNA}$-LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 950-990
- Print publication:
- December 2022
-
- Article
- Export citation
GÖDEL’S THEOREM AND DIRECT SELF-REFERENCE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 650-654
- Print publication:
- June 2023
-
- Article
- Export citation
THE JACOBSON RADICAL OF A PROPOSITIONAL THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 163-181
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVARIANCE CRITERIA AS META-CONSTRAINTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 104-132
- Print publication:
- March 2022
-
- Article
- Export citation
TEMPORAL INTERPRETATION OF MONADIC INTUITIONISTIC QUANTIFIERS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 164-187
- Print publication:
- March 2023
-
- Article
- Export citation
NON-CLASSICAL FOUNDATIONS OF SET THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 347-376
- Print publication:
- March 2022
-
- Article
- Export citation