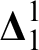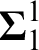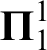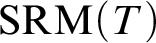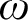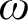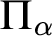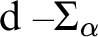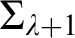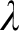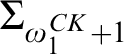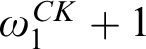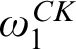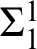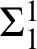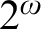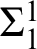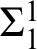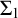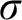Refine listing
Actions for selected content:
1095 results in 03xxx
RECURSIVE AXIOMATISATIONS FROM SEPARATION PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 03 February 2021, pp. 1228-1258
- Print publication:
- September 2021
-
- Article
- Export citation
COMBINING RESURRECTION AND MAXIMALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 02 February 2021, pp. 397-414
- Print publication:
- March 2021
-
- Article
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS – ERRATUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 2253-2255
- Print publication:
- November 2022
-
- Article
- Export citation
THE REVERSE MATHEMATICS OF THEOREMS OF JORDAN AND LEBESGUE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1657-1675
- Print publication:
- December 2021
-
- Article
- Export citation
TWO-VARIABLE LOGIC HAS WEAK, BUT NOT STRONG, BETH DEFINABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 785-800
- Print publication:
- June 2021
-
- Article
- Export citation
FINDING DESCENDING SEQUENCES THROUGH ILL-FOUNDED LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 817-854
- Print publication:
- June 2021
-
- Article
- Export citation
CONGRUENCE OF ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 746-761
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
$[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1632-1656
- Print publication:
- December 2021
-
- Article
- Export citation
CORES OVER RAMSEY STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 352-361
- Print publication:
- March 2021
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
SCOTT COMPLEXITY OF COUNTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1706-1720
- Print publication:
- December 2021
-
- Article
- Export citation
CHARACTERIZING EXISTENCE OF A MEASURABLE CARDINAL VIA MODAL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 162-177
- Print publication:
- March 2021
-
- Article
- Export citation
THE OPEN AND CLOPEN RAMSEY THEOREMS IN THE WEIHRAUCH LATTICE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 316-351
- Print publication:
- March 2021
-
- Article
- Export citation
ARONSZAJN TREE PRESERVATION AND BOUNDED FORCING AXIOMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 293-315
- Print publication:
- March 2021
-
- Article
- Export citation
Minimal definable graphs of definable chromatic number at least three
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e7
-
- Article
-
- You have access
- Open access
- Export citation
IDEAL INDEPENDENT FAMILIES AND THE ULTRAFILTER NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 128-136
- Print publication:
- March 2021
-
- Article
- Export citation
THE ORDER OF REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1555-1583
- Print publication:
- December 2021
-
- Article
- Export citation
THE Σ1-DEFINABLE UNIVERSAL FINITE SEQUENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 783-801
- Print publication:
- June 2022
-
- Article
- Export citation
SHORTENING CLOPEN GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1541-1554
- Print publication:
- December 2021
-
- Article
- Export citation
A MARRIAGE OF BROUWER’S INTUITIONISM AND HILBERT’S FINITISM I: ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 January 2021, pp. 437-497
- Print publication:
- June 2022
-
- Article
- Export citation