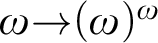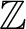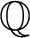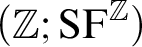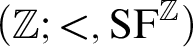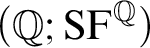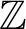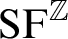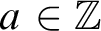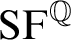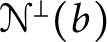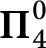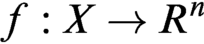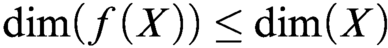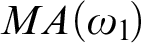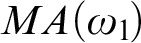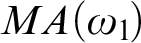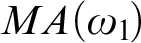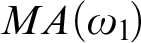Refine listing
Actions for selected content:
1095 results in 03xxx
RIGOUR AND PROOF
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 21 October 2020, pp. 480-508
- Print publication:
- June 2023
-
- Article
- Export citation
PROBABILISTIC STABILITY, AGM REVISION OPERATORS AND MAXIMUM ENTROPY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 553-590
- Print publication:
- September 2022
-
- Article
- Export citation
CLASSES OF BARREN EXTENSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 178-209
- Print publication:
- March 2021
-
- Article
- Export citation
INTRINSIC SMALLNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 558-576
- Print publication:
- June 2021
-
- Article
- Export citation
UNIFORM DEFINABILITY OF INTEGERS IN REDUCED INDECOMPOSABLE POLYNOMIAL RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1376-1402
- Print publication:
- December 2020
-
- Article
- Export citation
GENERIC CODING WITH HELP AND AMALGAMATION FAILURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1385-1395
- Print publication:
- December 2021
-
- Article
- Export citation
MODEL THEORY AND COMBINATORICS OF BANNED SEQUENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1-20
- Print publication:
- March 2022
-
- Article
- Export citation
THE ADDITIVE GROUPS OF
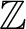 $\mathbb {Z}$ AND
$\mathbb {Z}$ AND 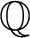 $\mathbb {Q}$ WITH PREDICATES FOR BEING SQUARE-FREE
$\mathbb {Q}$ WITH PREDICATES FOR BEING SQUARE-FREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1324-1349
- Print publication:
- December 2021
-
- Article
- Export citation
HOMOTOPY MODEL THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1301-1323
- Print publication:
- December 2021
-
- Article
- Export citation
DECIDABILITY OF ADMISSIBILITY: ON A PROBLEM BY FRIEDMAN AND ITS SOLUTION BY RYBAKOV
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1-38
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Q-WADGE HIERARCHY IN QUASI-POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 732-757
- Print publication:
- June 2022
-
- Article
- Export citation
RELATIONSHIPS BETWEEN COMPUTABILITY-THEORETIC PROPERTIES OF PROBLEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 47-71
- Print publication:
- March 2022
-
- Article
- Export citation
Some complexity results in the theory of normal numbers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 170-198
- Print publication:
- February 2022
-
- Article
- Export citation
A SCHEMATIC DEFINITION OF QUANTUM POLYNOMIAL TIME COMPUTABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 08 September 2020, pp. 1546-1587
- Print publication:
- December 2020
-
- Article
- Export citation
DIMENSION INEQUALITY FOR A DEFINABLY COMPLETE UNIFORMLY LOCALLY O-MINIMAL STRUCTURE OF THE SECOND KIND
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1654-1663
- Print publication:
- December 2020
-
- Article
- Export citation
SELF-REFERENTIAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1687-1716
- Print publication:
- December 2020
-
- Article
- Export citation
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
CONTINUOUS SENTENCES PRESERVED UNDER REDUCED PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 September 2020, pp. 649-681
- Print publication:
- June 2022
-
- Article
- Export citation
THE FUNDAMENTAL THEOREM OF CENTRAL ELEMENT THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1599-1606
- Print publication:
- December 2020
-
- Article
- Export citation
ON WIDE ARONSZAJN TREES IN THE PRESENCE OF MA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 210-223
- Print publication:
- March 2021
-
- Article
- Export citation