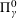 $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND 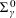 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
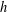 $h$ -IMPLICATIONS
$h$ -IMPLICATIONS