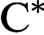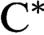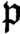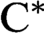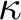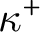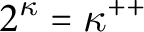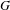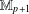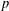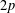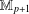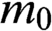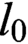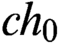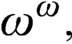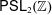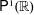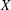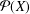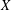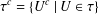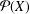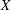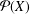Refine listing
Actions for selected content:
1095 results in 03xxx
COMPUTABLE LINEAR ORDERS AND PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 605-623
- Print publication:
- June 2020
-
- Article
- Export citation
DECIDING SOME MALTSEV CONDITIONS IN FINITE IDEMPOTENT ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 June 2020, pp. 539-562
- Print publication:
- June 2020
-
- Article
- Export citation
VOICULESCU’S THEOREM FOR NONSEPARABLE
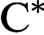 $\text{C}^{\ast} $-ALGEBRAS
$\text{C}^{\ast} $-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 624-631
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
DOMINATION AND REGULARITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 19 January 2021, pp. 103-117
- Print publication:
- June 2020
-
- Article
- Export citation
Sigma-Prikry forcing I: The Axioms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1205-1238
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Maximally highly proximal flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 18 May 2020, pp. 2220-2240
- Print publication:
- July 2021
-
- Article
- Export citation
A MINIMAL CONGRUENCE LATTICE REPRESENTATION FOR
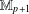 $\mathbb{M}_{p+1}$
$\mathbb{M}_{p+1}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 332-340
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON THE DIAGONAL LEMMA OF GÖDEL AND CARNAP
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 80-88
- Print publication:
- March 2020
-
- Article
- Export citation
AN APPLICATION OF RECURSION THEORY TO ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 15-25
- Print publication:
- March 2020
-
- Article
- Export citation
WEYL REEXAMINED: “DAS KONTINUUM” 100 YEARS LATER
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 26-79
- Print publication:
- March 2020
-
- Article
-
- You have access
- Open access
- Export citation
NONMEASURABLE SETS AND UNIONS WITH RESPECT TO TREE IDEALS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 19 June 2020, pp. 1-14
- Print publication:
- March 2020
-
- Article
- Export citation
MEASURABLE REALIZATIONS OF ABSTRACT SYSTEMS OF CONGRUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 February 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The expressiveness of quasiperiodic and minimal shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1086-1138
- Print publication:
- April 2021
-
- Article
- Export citation
On Baire measurable colorings of group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 818-845
- Print publication:
- March 2021
-
- Article
- Export citation
DIFFERENCE-MAKING CONDITIONALS AND THE RELEVANT RAMSEY TEST
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 12 December 2019, pp. 133-164
- Print publication:
- March 2022
-
- Article
- Export citation
SOME MODEL-THEORETIC RESULTS ON THE 3-VALUED PARACONSISTENT FIRST-ORDER LOGIC QCIORE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 09 December 2019, pp. 187-224
- Print publication:
- March 2021
-
- Article
- Export citation
Real closed valued fields with analytic structure
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 05 December 2019, pp. 249-261
-
- Article
-
- You have access
- Open access
- Export citation
Maximal hyperbolic towers and weight in the theory of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 479-498
- Print publication:
- May 2021
-
- Article
- Export citation
NATURAL FORMALIZATION: DERIVING THE CANTOR-BERNSTEIN THEOREM IN ZF
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 250-284
- Print publication:
- March 2021
-
- Article
- Export citation