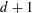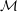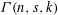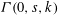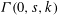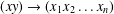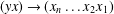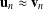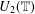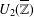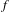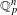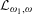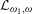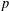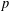Refine listing
Actions for selected content:
1095 results in 03xxx
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 561-590
- Print publication:
- May 2019
-
- Article
- Export citation
POLYCYCLIC, METABELIAN OR SOLUBLE OF TYPE (FP)∞ GROUPS WITH BOOLEAN ALGEBRA OF RATIONAL SETS AND BIAUTOMATIC SOLUBLE GROUPS ARE VIRTUALLY ABELIAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 13 March 2017, pp. 209-218
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
REDUCED POWERS OF SOUSLIN TREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 January 2017, e2
-
- Article
-
- You have access
- Open access
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
COMPACT SPACES OF THE FIRST BAIRE CLASS THAT HAVE OPEN FINITE DEGREE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 21 November 2016, pp. 1173-1196
- Print publication:
- November 2018
-
- Article
- Export citation
A FINITE-TO-ONE MAP FROM THE PERMUTATIONS ON A SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 177-182
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
KŐNIG’S LINE COLORING AND VIZING’S THEOREMS FOR GRAPHINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 September 2016, e27
-
- Article
-
- You have access
- Open access
- Export citation
INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 28 June 2016, e17
-
- Article
-
- You have access
- Open access
- Export citation
CONSISTENCY OF CIRCUIT EVALUATION, EXTENDED RESOLUTION AND TOTAL NP SEARCH PROBLEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 24 June 2016, e15
-
- Article
-
- You have access
- Open access
- Export citation
BROOKS’ THEOREM FOR MEASURABLE COLORINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 24 June 2016, e16
-
- Article
-
- You have access
- Open access
- Export citation
TWISTED GALOIS STRATIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 1-60
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
- Print publication:
- April 2018
-
- Article
- Export citation
DNR AND INCOMPARABLE TURING DEGREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 06 April 2016, e7
-
- Article
-
- You have access
- Open access
- Export citation
THE FINITE BASIS PROBLEM FOR THE MONOID OF TWO-BY-TWO UPPER TRIANGULAR TROPICAL MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 54-64
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Rational Values of Weierstrass Zeta Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 945-958
-
- Article
- Export citation
The Weyl–von Neumann theorem and Borel complexity of unitary equivalence modulo compacts of self-adjoint operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 29 October 2015, pp. 1115-1144
- Print publication:
- December 2015
-
- Article
- Export citation
A DEFINABLE
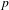 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
CATEGORICITY OF MODULAR AND SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1075-1101
- Print publication:
- November 2017
-
- Article
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
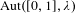
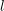


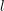

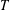
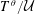
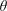
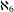
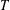
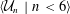
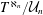
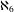
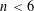
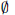 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.